Inspired From Inspiration
f ( x ) = 2 1 + 4 x − x 2 − 1 0 + 3 x − x 2
If the maximum value of the function given above occurs at x = x 0 and the maximum value is y 0 , find x 0 + y 0 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How did you draw the graph of the function?
Let S 1 = 2 5 − ( x − 2 ) 2 , S 2 = 4 4 9 − ( x − 2 3 ) 2
The given function f ( x ) = S 1 − S 2 is the difference in ordinates of the points lying on the two semicircles S 1 and S 2 having the same abscissa.
Now let's collect some data about the two semicircles. The semicircle S 2 has centre C 2 ( 2 3 , 0 ) , radius R 2 = 2 7 and is contained within semicircle S 1 which is centered at C 1 ( 2 , 0 ) with radius R 1 = 5 . Both lie above y-axis and the domain of the function is x ∈ [ − 2 , 5 ] .
The ordinate of such a semicircle decreases as we move the along the x-axis, away from the centre of the semicircle … { 1 }
Also, for the same change in x , due to a larger radius, magnitude of increase/decrease in S 1 is less than that in S 2 … { 2 }
From { 1 } , we conclude maximum value of f ( x ) occurs when we select an x which is farther away from C 2 and closer to C 1 ,i.e., x > 2 3
Also from { 2 } , we notice that as we move towards the right from x = 2 , S 2 decreases more rapidly than S 1 , thus the difference in their ordinates keep increasing in the interval x > 2 .
The maximum value permitted for x > 2 is x = 5 and hence, maximum value of the function is:
f ( 5 ) = 2 5 − ( 5 − 2 ) 2 − 0 = 1 6 = 4
Hence,
x 0 + y 0 = 5 + 4 = 9
Note :- For better visualisation:
1)Sketch the graphs of S 1 and S 2 .
2)Picture the part of the line x = k , k ∈ [ − 2 , 5 ] intercepted between S 1 and S 2 as k varies over it's domain.
Feel free to ask for any further clarification.
Great work (+1)
The graph of f ( x ) is given by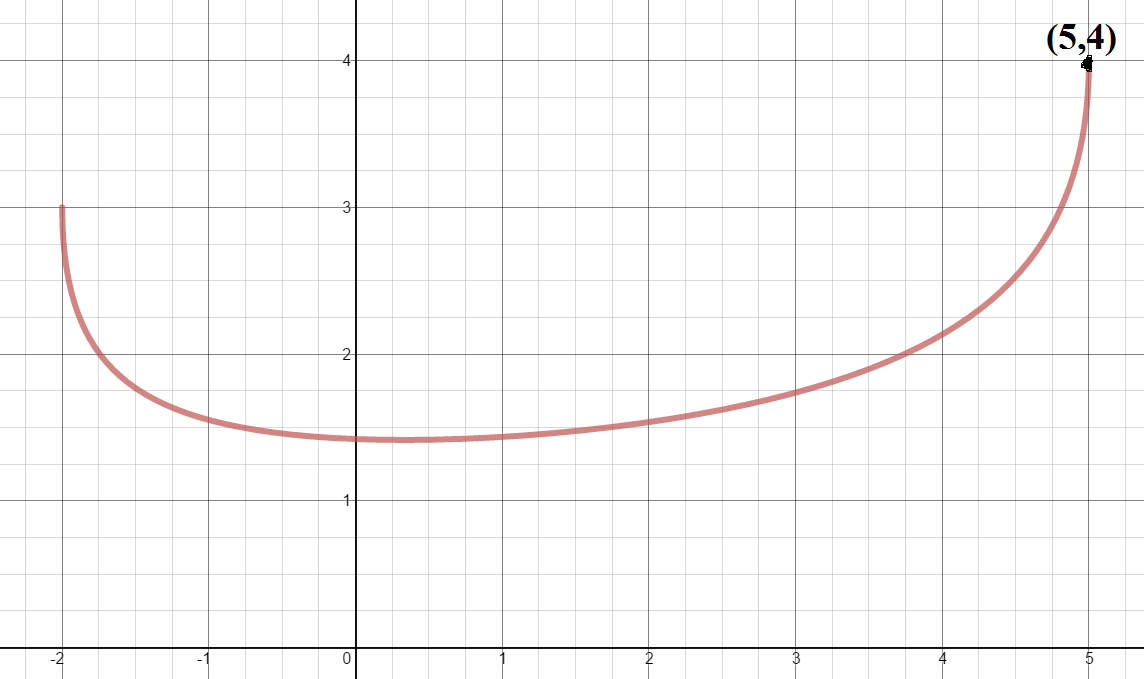 Graph
And the maximum value occurs at
x
0
=
5
and maximum value is
y
0
=
4
So our answer is
x
0
+
y
0
=
5
+
4
=
9
Graph
And the maximum value occurs at
x
0
=
5
and maximum value is
y
0
=
4
So our answer is
x
0
+
y
0
=
5
+
4
=
9