Inspired from Steven Sir!
Say we have a rectangular hyperbola, of which the right hand part is charged with linear charge density and the left one with .
There is a Rod Lying on the y-axis, with mass , Lenght and its center is kept at . It is charged with, say surface charge density, .
Check out the image.
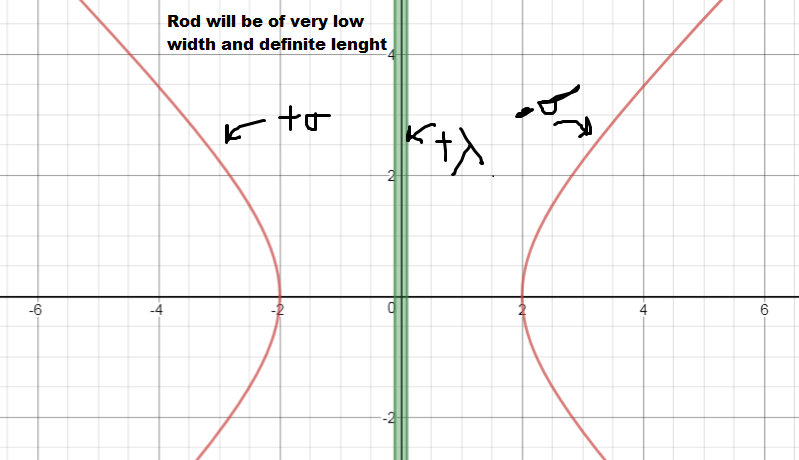
Find the magnitude acceleration of the rod, as soon as we release it.
If the acceleration of the rod is , Input .
Details And Assumption
-
Take , and , and
-
Hyperbola is indefinite.
-
Find the acceleration in
-
You can use Wolfram Alpha.
-
Orginial
-
Inspired from Steven Sir
The answer is 410.372632.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the position vector of a point on the vertical wire be:
r p = y j ^
And that on the upper half of the right branch of the hyperbola be:
r h = x i ^ + x 2 − 4 j ^
The vector joining these two points directed away from the wire is:
r = r h − r p
We consider a line element on the wire. The length of the element near the given position vector has charge λ d y . We also consider an arc length element on the hyperbola. The charge on that element near the given position vector is σ d s where d s is the arc length magnitude which is:
d s = d x 1 + ( d x d y ) 2
For the upper half of the right lobe:
d s = d x x 2 − 4 2 x 2 − 4
Applying Columb's law to find electrostatic force at wire element due to the hyperbolic element:
d F = ∣ r ∣ 3 K ( λ d y ) ( σ d s ) r
K = 4 π ϵ o 1
d F = d F x i ^ + d F y j ^
Substituting all expressions and simplifying gives:
d F x = ⎝ ⎜ ⎛ ( ( y − x 2 − 4 ) 2 + x 2 ) 3 / 2 K λ σ 2 x 2 ( x 2 − 4 ) 2 x 2 − 4 ⎠ ⎟ ⎞ d x d y
Similarly an expression for d F y can be computed. Now, the total force on the wire due to the upper half of the right lobe of the hyperbola is:
F x = ∫ − 2 2 ∫ 2 ∞ ⎝ ⎜ ⎛ ( ( y − x 2 − 4 ) 2 + x 2 ) 3 / 2 K λ σ 2 x 2 ( x 2 − 4 ) 2 x 2 − 4 ⎠ ⎟ ⎞ d x d y
Therefore, by symmetry, the force due to the entire right lobe of the hyperbola will be:
F R = 2 F x
Again, by symmetry, the force due to both lobes along the x-direction will be:
F T = 2 F R = 4 F x
Therefore, the acceleration A is:
A = M F T
All forces along Y will evaluate to zero. One can check this by even evaluating the integrals. This step is left out here.
Having obtained F T , the answer comes out to be:
2 0 K A ≈ 4 1 0 . 3 7 3