Inspired my myself!
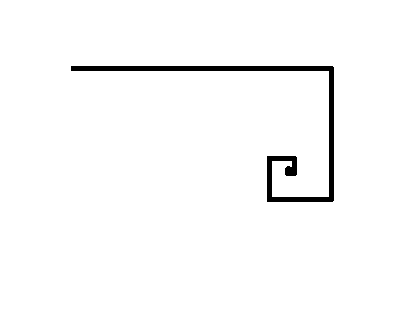 A particle is on the point
(
3
,
5
)
on the plane. It goes 10 units in the direction of positive
x
-axis. Then it turns towards right making an angle of 90 degrees with its initial direction and goes ahead 5 units, Now it again takes a right turn and goes ahead 2.5 units. It keeps turning right and travels half the distance traveled in the turn just before it . This goes on without end. Find the final distance of the particle from the origin
(
0
,
0
)
?
A particle is on the point
(
3
,
5
)
on the plane. It goes 10 units in the direction of positive
x
-axis. Then it turns towards right making an angle of 90 degrees with its initial direction and goes ahead 5 units, Now it again takes a right turn and goes ahead 2.5 units. It keeps turning right and travels half the distance traveled in the turn just before it . This goes on without end. Find the final distance of the particle from the origin
(
0
,
0
)
?
The answer would come in the form square root of x , submit your answer as x .
The answer is 122.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Start the process with respect to origin(i.e let the particle started from origin instead of (3,5)).Now work for the final X- Coordinate and final Y-Coordinate of the particle independently.Final X coordinate is the sum of the infinite geometric progression 10,-10/4,10/16,-10/64........=10/(1+1/4)=8 .Similarly, Final Y-Coordinate is the sum of the infinite GP 5,-5/4,5/16.........=4. But the particle started towards right with initial X-Coordinate 3 => actual final X-Coordinate=3+8=11. And actual final Y-Coordinate =5-4 =1 as the particle started down with respect to (3,5) initially.Hence required 'x'=11^2+1^2=122
I missed. For y, I added 5+4=9 instead of 5-4=1!! We can see this is a G.S. with r = − 4 1 . F o r x , a = 1 0 S u m = 1 + 4 1 1 0 = 8 . F o r y , r a t i o r e m a i n t h e s a m e , a = − 5 , ∴ i t i s h a l f o f x . S u m = − 4 . T h e c o o r d i n a t e s a r e ( 3 + 8 , 5 − 4 ) = ( 1 1 , 1 ) . ∴ x = 1 1 2 = 1 2 = 1 2 2 .
To Deepak Kumar, Maybe, you've made a typo. The particle started down with respect to (3,5) initially. Everything else is correct.
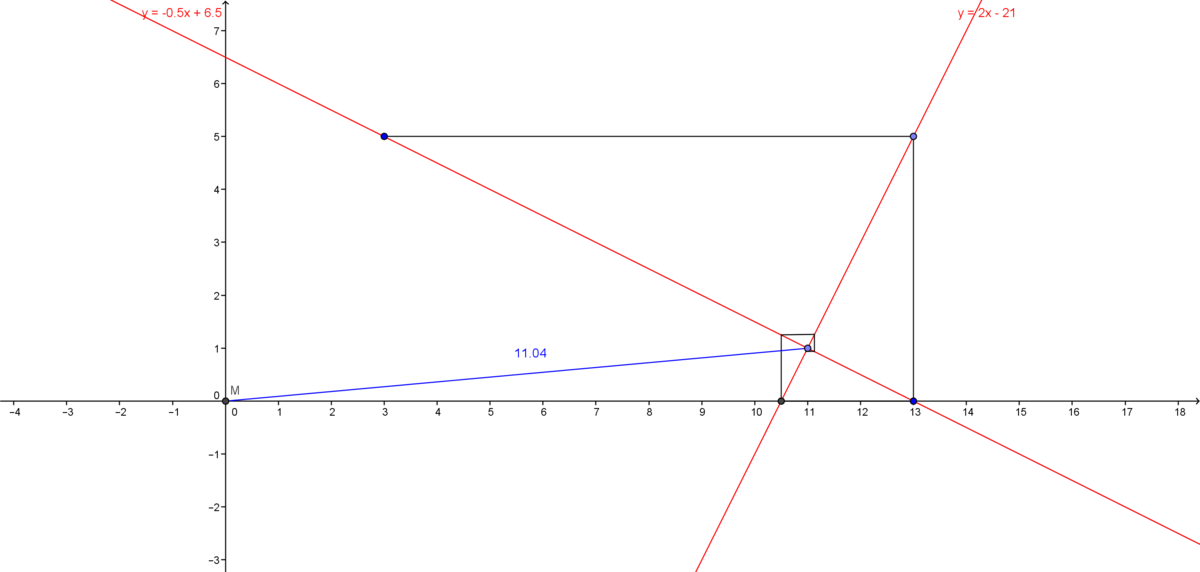
Solving graphically by simultaneous equations and distance formula
That was really a nice problem...
Let the coordinates of the final point be P ( X , Y ) . Therefore, the distance of the particle at the final point P from the origin O is O P = X 2 + Y 2 = x ⇒ x = X 2 + Y 2 .
Therefore, we are supposed to enter the value of X 2 + Y 2 as the answer.
( 3 , 5 ) are the coordinates of the initial point.
The Coordinates change as the particle moves, the x-coordinate varies as X = 3 + 1 0 − 2 2 1 0 + 2 4 1 0 − 2 6 1 0 + … ∞ X = 3 + Infinite Converging G.P. Series with the First term, a=10, Common Ratio, r=-1/4 X = 3 + a 1 − r 1 = 3 + 1 0 1 − ( − 4 1 ) 1 = 3 + 8 ⇒ X = 1 1
Similarly, Y = y 0 − 2 1 0 + 2 3 1 0 − 2 5 1 0 + … ∞ Y = 5 − 2 1 0 × 1 − 4 1 1 = 5 − 4 ⇒ Y = 1
Therefore, x = X 2 + Y 2 = 1 1 2 + 1 2 = 1 2 2 :D
P.S. Change in Coordinates of the position of the particle explained : As the particle moves firstly 10 units along the positive x direction, x coordinate increases by 10 units. Further when the particle turns to the right i.e. towards negative y direction and moves 1 0 / 2 = 5 units, the y co-ordinate decreases by 5 units. Now as the particle turns to the right, it faces the negative x direction, and moves by 1 0 / ( 2 2 ) = 2 . 5 units, the x-coordinate decreases by 2.5 units. The process goes on. The changes can be listed as (x co-ordinate increases by 10 units, y co-ordinate decreases by 5 units, x co-ordinate decreases by 2.5 units,...) Clubbing changes in x coordinate together, we get (x co-ordinate increases by 10 units, x co-ordinate decreases by 2.5 units, ...). Clubbing changes in y coordinate together, we get (y co-ordinate decreases by 5 units, y co-ordinate increases by 1.25 units, ...). Applying these changes to the initial coordinates, gives us the position of the final point.
Let's look at the x the y separately.:
The initial x value is 3, and because the particle only moves horizontally every other iteration and alternating positive and negative direction, the change in x can be represented by the geometric series ∑ n = 0 ∞ 1 0 ( 4 − 1 ) n
This series converges to 1 − 4 − 1 1 0 which simplifies to 8 , so our final x coordinate is 3 + 8 = 1 1
The initial y value is 5, and for the same reasons as above, the change in y can be represented by ∑ n = 0 ∞ − 5 ( 4 − 1 ) n
This series converges to 1 − 4 − 1 − 5 which simplifies to − 4 , so our final y coordinate is 5 − 4 = 1
Therefore, the particle ends up at ( 1 1 , 1 )
To find the distance from the origin to this point we just use the distance formula.
( 1 1 − 0 ) 2 + ( 1 − 0 ) 2 = 1 2 2 , so our answer is 1 2 2