Insufficient Information in Geometry?

In the above diagram,
A
B
C
D
is a square and point
E
lies on side
C
D
.
Line segment
A
E
and diagonal
B
D
intersect at point
F
, such that
B
F
:
F
D
=
4
:
3
.
If the combined area of the 2 blue triangles is 1 0 0 cm 2 , find the area of the square in cm 2 .
Note:
The figure is not drawn to a scale
The answer is 224.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
From the text, we know that F D : B F = 3 : 4 c m . And the ratio between two similar triangles is the ratio between the square of the sides of the triangles.
We have [ B A F ] [ D E F ] = B F 2 F D 2 = 1 6 9 .
Now, we can find the area of [ D E F ] and [ B A F ] , since we have [ D E F ] + [ B A F ] = 1 0 0 c m 2 .
[ D E F ] = 9 + 1 6 9 × 1 0 0 = 3 6 c m 2 .
[ B A F ] = 1 0 0 − 3 6 = 6 4 c m 2 .
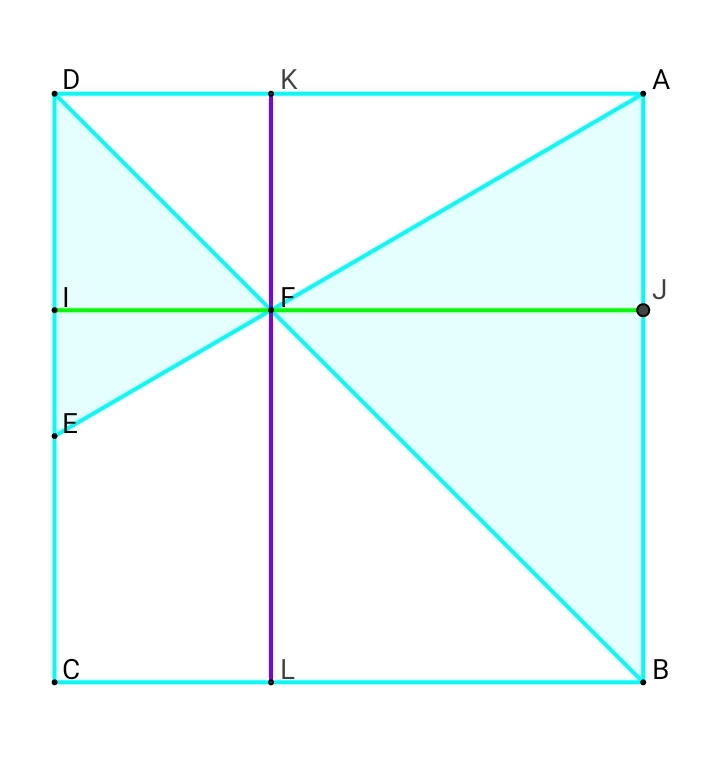
We can draw a line I J which is parallel to A D , and a line K L which is parallel to A B and prependicular to I J as you can see in the figure.
Let the side of the square is a and C E = x c m , which means D E = ( a − x ) c m . We let the height of △ D E F = t 1 c m and the height of △ B A F = t 2 c m .
We can see that [ B A F ] 6 4 a t 2 = 2 a t 2 = 2 a t 2 = 1 2 8 c m 2 .
So, we have [ A B L K ] = 1 2 8 c m 2 .
We can see that △ D E F and △ B A F are similar to each other. Then we have
a a − x = B F F D = 4 3
3 a = 4 a − 4 x ⇒ x = 4 1 a .
We know that [ D E F ] = 2 D E × t 1 ⇒ 3 6 = 2 ( a − x ) t 1 .
3 6 7 2 4 3 a t 1 a t 1 = 2 ( a − x ) t 1 = ( a − 4 1 ) t 1 = 7 2 = 9 6 c m 2 .
Now, we have [ D K L C ] = 9 6 c m 2 .
Hence, we have [ A B C D ] = [ A B L K ] + [ D K L C ] = 1 2 8 + 9 6 = 2 2 4 c m 2
We can do like this also: Let AB=x , JF=y | 1/2 × xy = 64 Therefore xy=128 | Area of Square = AB x BC = AB x ( JK + IF) | = x * (y+3/4y) = 7xy/4 = 7*128/4 = 224 cm²
Log in to reply
Great! You have another simple way to solve this! Nice..
Its JF instead of JK and 3y/4 instead of 3/4y.. Sorry 😜
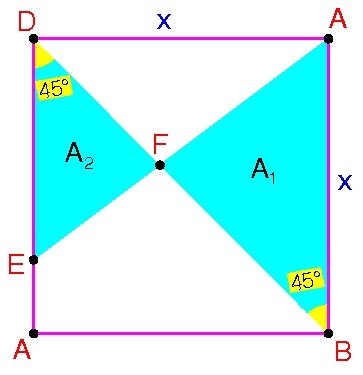 Let
x
be the side length of the square. By pythagorean theorem,
B
D
=
x
2
. Then,
B
F
=
7
4
x
2
and
F
D
=
7
3
2
. Since
△
D
F
E
is similar to
△
B
F
A
,
x
D
E
=
F
B
D
F
⟹
D
E
=
4
3
x
.
Let
x
be the side length of the square. By pythagorean theorem,
B
D
=
x
2
. Then,
B
F
=
7
4
x
2
and
F
D
=
7
3
2
. Since
△
D
F
E
is similar to
△
B
F
A
,
x
D
E
=
F
B
D
F
⟹
D
E
=
4
3
x
.
Solving for the areas of the blue region, we have
A 1 = 2 1 ( x ) ( 7 4 ) x 2 s i n 4 5 = 0 . 2 8 5 7 1 4 2 8 5 x 2
A 2 = 2 1 ( 4 3 x ) ( 7 3 ) x 2 s i n 4 5 = 0 . 1 6 0 7 1 4 2 8 5 x 2
Adding the areas, we have
0 . 2 8 5 7 1 4 2 8 5 x 2 + 0 . 1 6 0 7 1 4 2 8 5 x 2 = 1 0 0
0 . 4 4 6 4 2 8 5 7 x 2 = 1 0 0
x 2 = 2 2 4 c m 2

Let a be the length of sides of the square.
Obviously ΔABF~ΔDEF . Therefore, BF:FD=4:3=AB:DE=H:h (where, H is height of ΔABF with base AB & h is height of ΔDEF with base DE). Note that H+h=a
We can write, DE=(3/4)*AB=3a/4, H=4a/7 & h=3a/7
Now, Combined Area of Blue Triangles =Ar(ΔABF)+Ar(ΔDEF)=(1/2)×(AB×H+DE×h)=(1/2) {(a) (4a/7)+(3a/4)×(3a/7)}=(2/7+9/56) a^2= (25/56) a^2 =100 sq.cm (given)
Hence, Area of square ABCD =a^2=100*56/25= 224 sq.cm
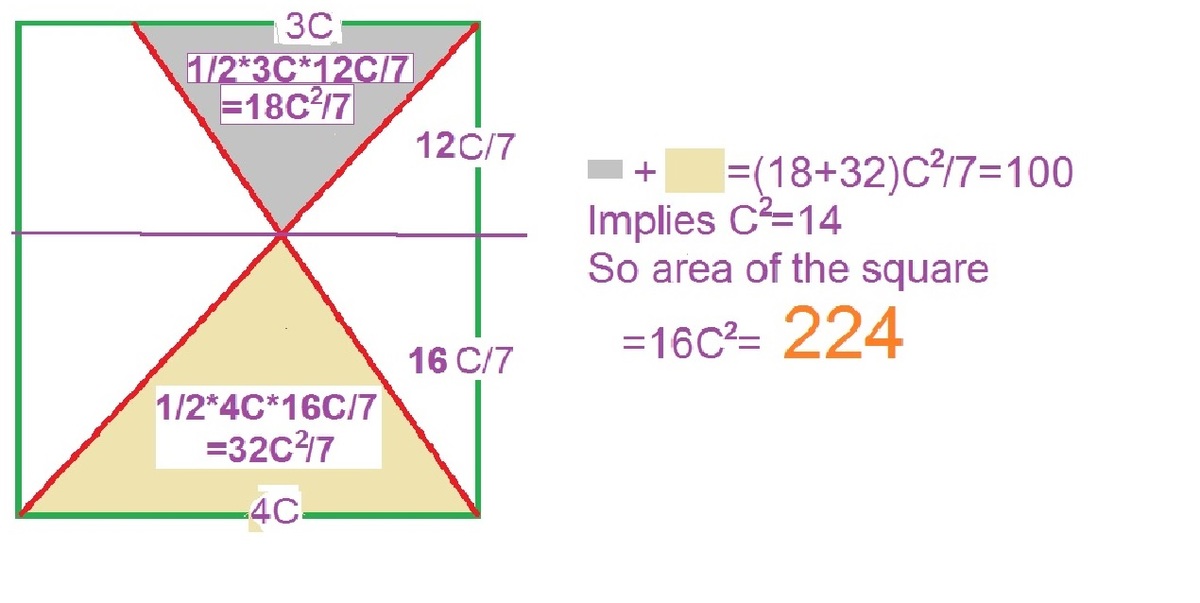
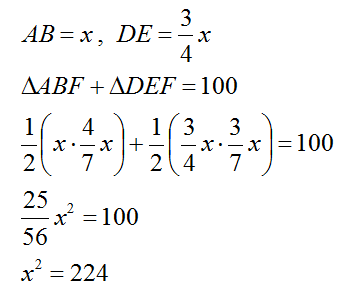
1 0 0 1 0 0 x = 1 6 x + 9 x = 2 5 x = 4
This will gives us [ B A F ] = 1 6 x = 1 6 × 4 = 6 4 .
Since [ B F ] : [ F D ] = 4 : 3 , [ D F A ] = 4 3 × 6 4 = 4 8 .
Hence, [ A B D ] = [ D F A ] + [ B A F ] = 6 4 + 4 8 = 1 1 2
Since [ A B D ] is half of the square, hence the square area is 2 × 1 1 2 = 2 2 4 .