Integers Inside

A regular n-gon has an interior angle of

$\dfrac {180(n-2)}{n}$ .

Rearranging, we get

$180 - \dfrac{360}{n}$

We have to know how many integers divide into 360, subtract it by two (because there are no polygons with 1 or 2 sides), and we get our answer

Number theory magic:

$360 = 2^{3}3^{2}5^{1}$

therefore $360$ has

$(3+1)(2+1)(1+1) = 4\cdot3\cdot2 = 24$ divisors

subtract two, we get $\boxed{22}$ :D

Each interior angle, of a regular polygon is $\dfrac{(n-2)180}{n}$ .

This value is an integer, so let us assume it to be $x$ .

So, $\dfrac{(n-2)180}{n}=x$ $\Rightarrow\space \dfrac{180n-360}{n}=x$ $\Rightarrow\space \dfrac{180n}{n}-\space \dfrac{360}{n}=x$ $\Rightarrow\space 180-\dfrac{360}{n}=x$ So, $x$ is an integer only if $360$ divides $n$ . So, $n$ can have the following values: $1,2,3,4,5,6,8,9,10,12,15,18,20,24,30,36,40,45,60,72,90,120,180\space \text{and}\space 360.$ A polygon has a minimum of $3$ sides. So, $1$ and $2$ are excluded from the list of solutions, leaving a total of $\boxed{22}$ polygons.

If an interior angle of a regular polygon is an integer, then the exterior angle of a regular polygon is also an integer (since both add up to the integer $180°$ ).

Since each exterior angle is $\frac{360}{n}$ , the number of integer solutions would be the number of factors of $360$ that are greater or equal to $3$ (since a polygon must have at least $3$ sides) which include $3$ , $4$ , $5$ , $6$ , $8$ , $9$ , $10$ , $12$ , $15$ , $18$ , $20$ , $24$ , $30$ , $36$ , $40$ , $45$ , $60$ , $72$ , $90$ , $120$ , $180$ , and $360$ , for a total of $\boxed{22}$ .

Look at all of you with your fancy math. I just took a minute to write a python script to add them all up!

count = 0
for side in range(3,361):
    intAngle = 180-360/side
    if intAngle == int(intAngle):
        count = count + 1
        print(count,intAngle)

Similar to the solutions that enumerate the possible solutions by hand or with a simple Python program, we could use an Excel spreadsheet.

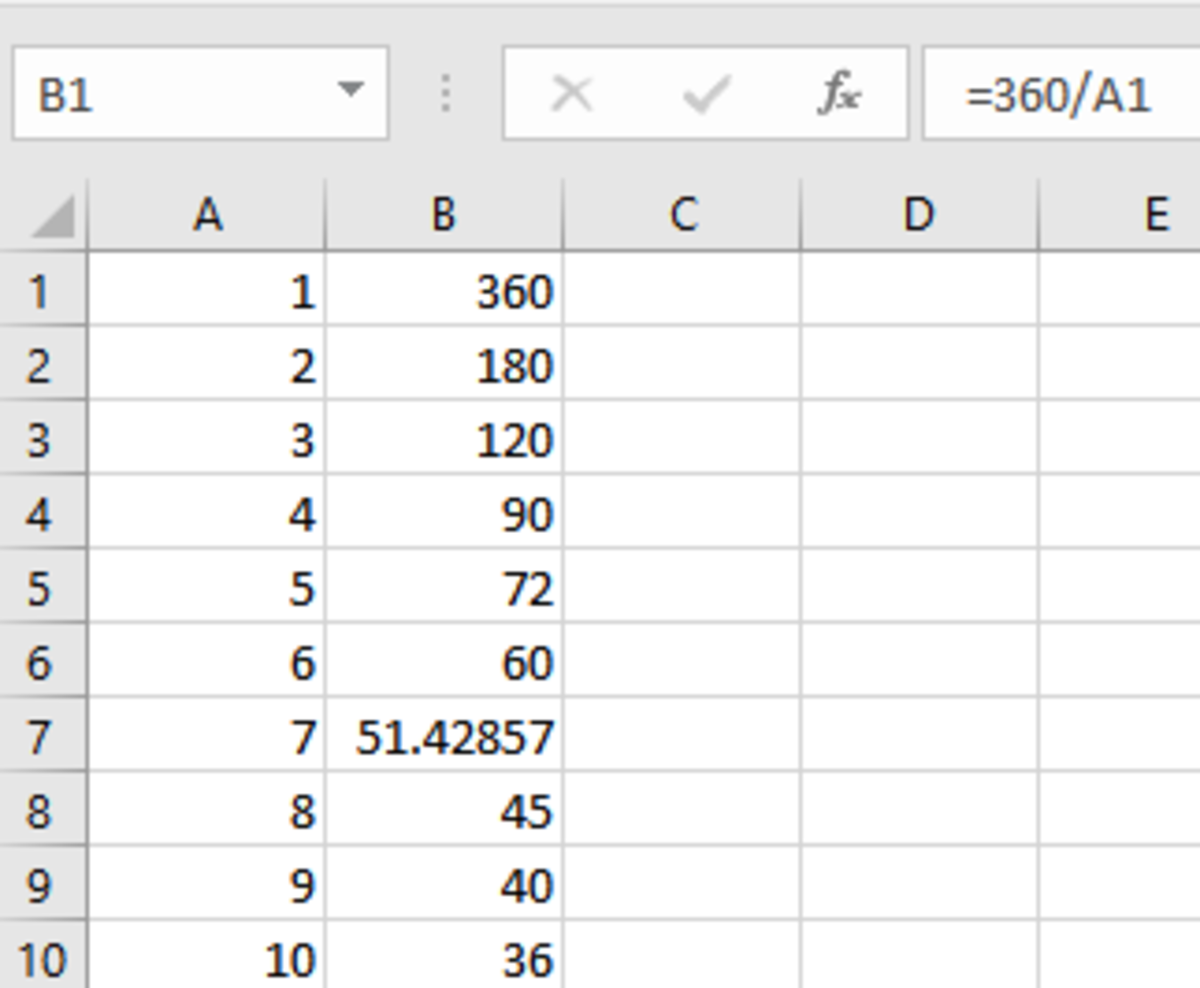
1. Set column A to the sequence of integers 1-360 (set A1=1, A2=2, then select these two cells and extend the sequence down by dragging the fill handle to A360 then releasing).
2. Set B1 to the formula =360/A1 then extend that formula down column B to B360.
3. Count the values in column B that are integers and subtract 2 (because n=1 and n=2 are not valid regular polygons).

The first 10 rows would look like:

Shortcut--Note that:

1. There can be no integer values of 360/n for n between 181 and 359, so you could set column A to 1-180 instead of 1-360 , then add one extra cell (A181) with value 360.
2. Instead of counting the integer values you could automate that. One easy way would be:
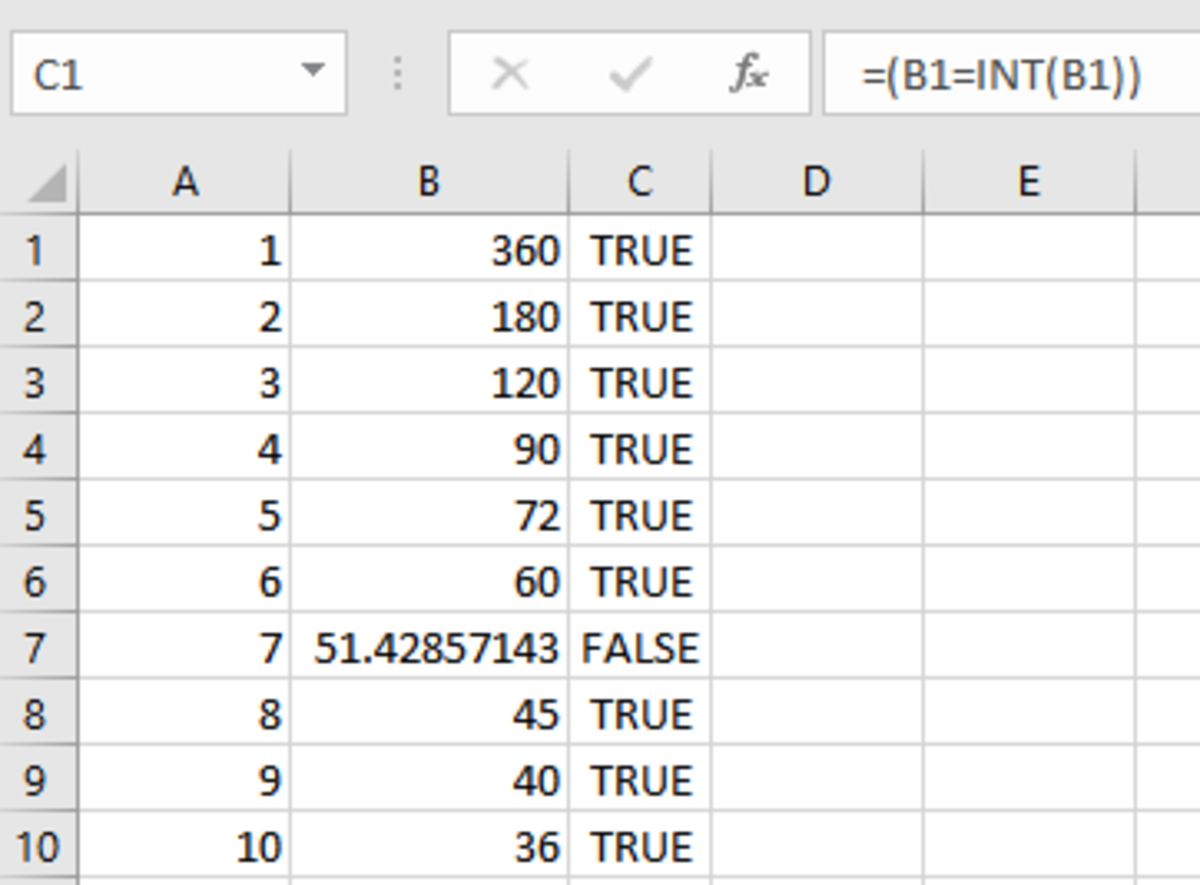
3. Set C1 to formula =(B1=INT(B1)) -- testing whether B1 is an integer.
4. Extend the formula in C1 down to C 360 (or C181 if you used the shortcut).

The first 10 rows will now look like:

1. In the first cell past the current end of column C data (so either C361 or C182) enter the formula =(COUNTIF(C1:C???,TRUE) where ??? is either 361 or 182.
2. If you drag down from C1 to C??? you won't have to enter the range by hand.
3. You can include the "- 2" in the formula, so set C361 or C182 to =(COUNTIF(C1:C???,TRUE) - 2) .

The last several rows would now look like:

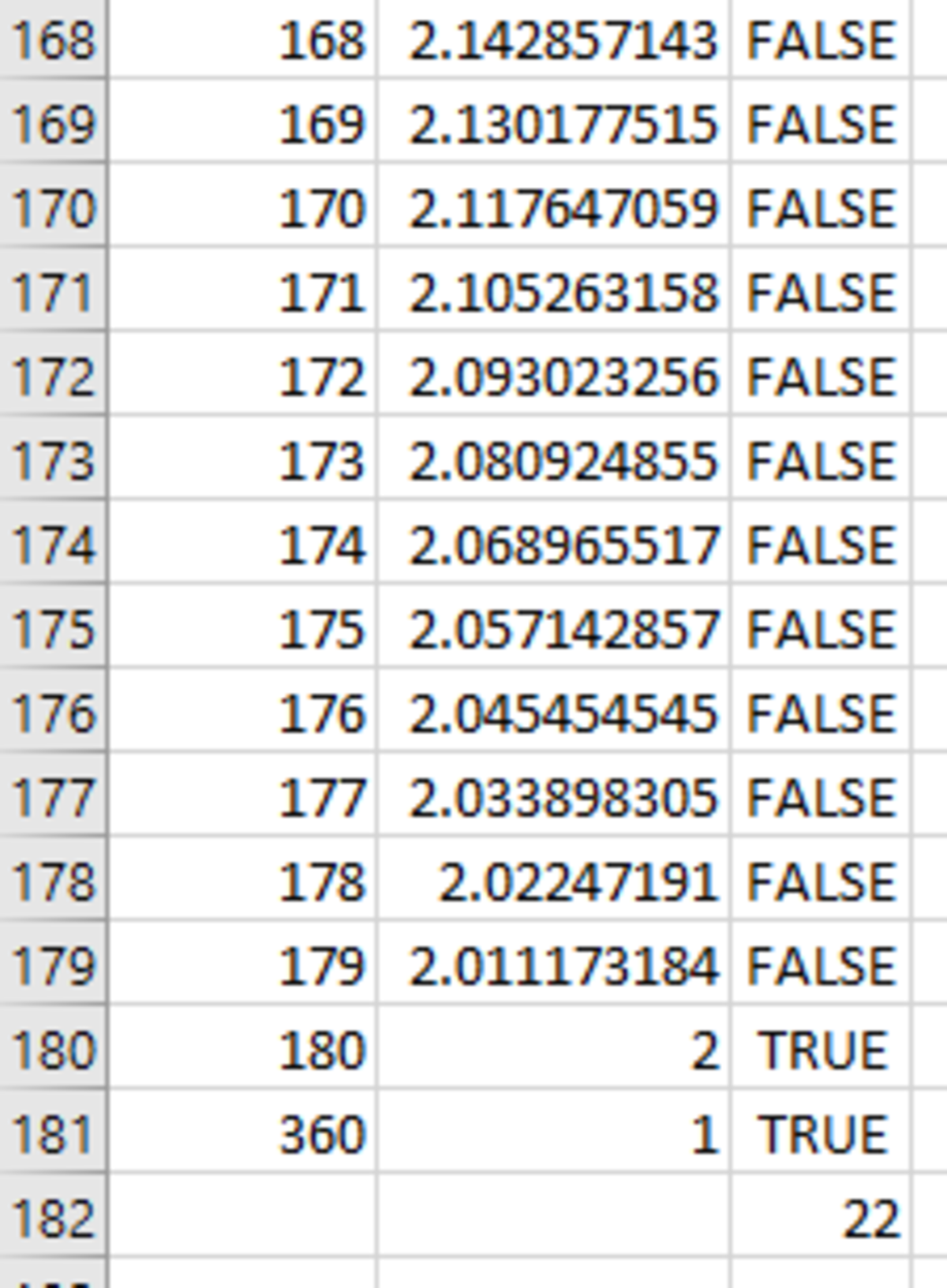
And the answer is $\boxed{ 22}$

The interior angles will be integers iff the exterior angles are integers.

The exterior angle of a regular n-gon is $\frac{360}{n}$ .

$\frac{360}{n}$ is an integer if n is a factor of 360.

360 = $2^{3}3^{2}5^{1}$ and so has $4 \times 3 \times 2 = 24$ factors.

However the factors 1 and 2 do not correspond to polygons (because there are no polygons with only one or only two sides).

And so there are $\boxed{22}$ polygons with the required property.

Notes

iff is not a spelling mistake. It is usual mathematical shorthand for 'if and only if'.

The 'exterior angle' is the angle found by extending one side and finding the angle between the extended line and the next side of the polygon.

To see that the exterior angle of a regular polygon is $\frac{360}{n}$ , hold your pen along one side of the polygon. Always rotating in the same direction, rotate your pen through one exterior angle so that it lines up with the next side. Repeat this so that your pen lines up successively with all n sides of the polygon and returns to its starting position. You will find that it has turned through n exterior angles and made one full revolution of 360 degrees! This holds for any convex polygon, regular or not. For regular polygons we know that each exterior angle is equal, and so each one must be $\frac{360}{n}$ as claimed. I highly recommend trying out the pen rotation proof on the diagrams provided in the question - it is very satisfying and totally convincing.

I used a quick way to find the number of factors of a number. Factorise the number as powers of prime numbers. Add one to each of the exponents. Then multiply the resulting numbers.

Minimal modication of the standard solution: If the internal angle is of a n-polygon is given by $180(n - 2)/n$ is to be an integer there must exist some integer $k$ such that $\frac{180(n - 2)}{n} = k$ and this can be rearranged into $180(n - 2) = kn$

$180n - 360 = kn$

and finally

$\color{magenta}(180 - k)n = 360$

I think this form more directly exposes to me that solutions (n,k) cossespond to different ways of factoring 360.

For example the product $4 \cdot 90 = 360$ corresponds to the solution $k = 174, n = 90$ which corresponds to the 90-sided polygon.

So we count the different ways of factoring 360 by the divisor-counter function

$\tau(360) = \tau(2^3 \cdot 3^2 \cdot 5) = (3 + 1)(2 + 1)(1 +1) = 24$

but then we have to discard the products

$360 \cdot 1 = 360$ and $180\cdot 2 = 360$

as $n = 1$ and $n = 2$ do not correspond to actual polygons.

24 - 2 = 22

1
2
3
4
5

x = 0
for n in range(3, 361):
    if (180-360/n)%1 == 0:
        x+=1
print(x)

This gives 22.

For those who like a more graphical solution:

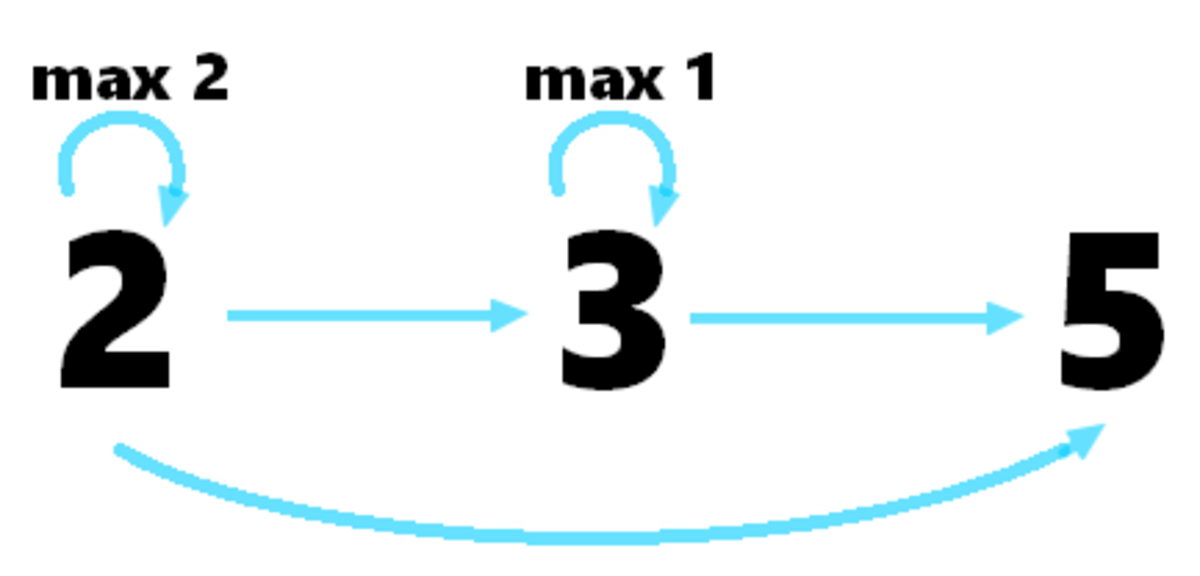
This is a directed graph with each node one of the primes when factorizing 360: $2^3 * 3^2 * 5$ . Now, starting at any node, count the paths of any length (min = 1, max = 5). You'll count a total of 20. Finally, add 3 and 5 as a solution too (2 isn't because we need at least 3 sides) and you'll end up with 22 solutions.

It's not a mathematical solution, but quite intuitive to understand the problem

You can list those polygons and their interior angles in Python like that:

for n in range(3, 1000):
    a = (n - 2) * 180 / n
    if float(a).is_integer():
        print("{} sides -- {}°".format(n, a))

Or short:

len([n for n in range(3, 1000) if float((n - 2) * 180 / n).is_integer()])

n = 20 does not give a 20-gon. any n greater than 20 gives negative angles and builds the same polygons. The correct answer is 11 polygons

check when the modulo of an integer and 360 equals 0 (i mod 360 == 0) and count for how many i’s this is the case. The answer is 22.

For all these shapes the size of each interior angle, i, times the number of angles, n gives you 360, i*n=360. This means we just have to look at all the factors of 360, obviously we have to discount a 1 or 2 sided shape, so the answer is the number of factors of 360, minus 2

360 has 22 divisors: 1,2,3,4,5,6,8,9,10,12,15,18,20,24,30,36,40,45,60,72,90,120,180, and 360.

Therefore, there are 22 regular shapes whose interior angles will divide 360 degrees evenly.