integral_03

let $x=\frac { u }{ 2 } \Rightarrow dx=\frac { du }{ 2 }$

$I=\int _{ 0 }^{ \infty }{ \frac { { x }^{ 6 } }{ 1+256{ x }^{ 8 } } dx } =\frac { 1 }{ { 2 }^{ 7 } } \int _{ 0 }^{ \infty }{ \frac { { u }^{ 6 } }{ 1+u^{ 8 } } } du$

$I=\frac { 1 }{ { 2 }^{ 7 } } \int _{ 0 }^{ \infty }{ \frac { 1 }{ 1+u^{ 8 } } } du\qquad //\int _{ 0 }^{ \infty }{ f\left( x \right) dx } =\int _{ 0 }^{ \infty }{ \frac { f\left( \frac { 1 }{ x } \right) }{ { x }^{ 2 } } dx }$

$I=\frac { 1 }{ { 2 }^{ 7 } } \cdot \frac { \pi }{ 8\cdot \sin { \left( \frac { \pi }{ 8 } \right) } } =\frac { \pi }{ { 2 }^{ 10 }\cdot \sin { \left( \frac { \pi }{ 8 } \right) } }$ //see Note(1)

$I=\frac { \pi }{ { 2 }^{ 10 }\cdot \frac { 1 }{ 2 } \sqrt { 2-\sqrt { 2 } } } =\frac { 1\pi }{ { 2 }^{ 9 }\sqrt { 2-\sqrt { 2 } } }$ \ //see Note(2)

$a=1, b={ 2 }^{ 9 }, c=2, d=2$

$a\times b\times c\times d={ 2 }^{ 11 }=2048$

Note(1) :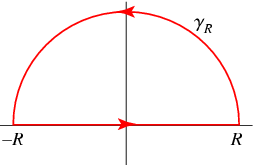

$\int _{ 0 }^{ \infty }{ \frac { 1 }{ 1+{ x }^{ 2n } } dx }$ * we will use contour integration *

$\oint { \frac { 1 }{ 1+{ z }^{ 2n } } dz= } \int _{ -R }^{ R }{ \frac { 1 }{ 1+{ x }^{ 2n } } dx } +\int _{ \gamma R }^{ }{ \frac { 1 }{ 1+{ z }^{ 2n } } dz }$

as $R\rightarrow \infty \qquad \int _{ \gamma R }^{ }{ \frac { 1 }{ 1+{ z }^{ 2n } } dz } =0$ //seepoof(a)

$\oint { \frac { 1 }{ 1+{ z }^{ 2n } } dz= } 2\pi i\cdot \sum _{ { z }_{ k }\in A }^{ }{ Res\left( f\left( { z }_{ k } \right) \right) } \qquad$ //A is the set of all poles inside contour // Residue Theorem

$\oint { \frac { 1 }{ 1+{ z }^{ 2n } } dz= } 2\pi i\cdot \frac { 1 }{ 2ni\cdot \sin { \left( \frac { \pi }{ 2n } \right) } } =\frac { 2\pi }{ 2n\sin { \left( \frac { \pi }{ 2n } \right) } }$ //see poof(b)

Now

$\oint { \frac { 1 }{ 1+{ z }^{ 2n } } dz= } \int _{ -R }^{ R }{ \frac { 1 }{ 1+{ x }^{ 2n } } dx } +\int _{ \gamma R }^{ }{ \frac { 1 }{ 1+{ z }^{ 2n } } dz }$

$asR\rightarrow \infty \frac { 2\pi }{ 2n\sin { \left( \frac { \pi }{ 2n } \right) } } =\int _{ -\infty }^{ \infty }{ \frac { 1 }{ 1+{ x }^{ 2n } } dx } +0$

$\Rightarrow \int _{ 0 }^{ \infty }{ \frac { 1 }{ 1+{ x }^{ 2n } } dx } =\frac { \pi }{ 2n\sin { \left( \frac { \pi }{ 2n } \right) } }$

poof(a):

$\left| \int _{ \gamma R }^{ }{ \frac { 1 }{ 1+{ z }^{ 2n } } dz } \right| \le ML$

//where $M=\max { \left| \frac { 1 }{ 1+{ z }^{ 2n } } \right| }$ and L is the length of $\gamma R=\pi R$ which is Half circle

$\left| { z }^{ 2n }+1 \right| \ge \left| { \left| z \right| }^{ 2n }-\left| 1 \right| \right| =\left| { R }^{ 2n }-1 \right| ={ R }^{ 2n }-1$ // $\left| z \right| =R$ and R>1

$\Rightarrow \left| \frac { 1 }{ 1+{ z }^{ 2n } } \right| \le \frac { 1 }{ { R }^{ 2n }-1 } \Rightarrow \left| \frac { 1 }{ 1+{ z }^{ 2n } } \right| \le \max { \left| \frac { 1 }{ 1+{ z }^{ 2n } } \right| } \le \frac { 1 }{ { R }^{ 2n }-1 }$

as $R\rightarrow \infty$ $\left| \int _{ \gamma R }^{ }{ \frac { 1 }{ 1+{ z }^{ 2n } } dz } \right| \le ML\le \frac { \pi R }{ { R }^{ 2n }-1 } =0$

poof(b):

let $z={ re }^{ i\theta }\Rightarrow { z }^{ 2n }=r$

so when $1+{ z }^{ 2n }=0\Rightarrow 1+r{ e }^{ i2n\theta }=0\Rightarrow r{ e }^{ i2n\theta }=-1$

$\Rightarrow$ r=1 and $\\cos { \left( 2n\theta \right) } =-1\Rightarrow 2n\theta =\left( 2k+1 \right) \pi \Rightarrow \theta =\frac { 2k+1 }{ 2n } \pi$ for k=0,1,2,......,2n-1

But we will take value of k from 0 to (n-1) because the other poles are outside contour \ when k=n $\Rightarrow \theta =\frac { 2n+1 }{ 2n } \pi >\pi$

$Res\left( f\left( { z }_{ k } \right) \right) =\lim _{ z\rightarrow { z }_{ k } }{ \left( \left( z-{ z }_{ k } \right) \cdot \frac { 1 }{ 1+{ z }^{ 2n } } \right) } =\lim _{ z\rightarrow { z }_{ k } }{ \left( \frac { 1 }{ 2n\cdot { z }^{ 2n-1 } } \right) } =\frac { { z }_{ k } }{ 2n\cdot { { z }_{ k } }^{ 2n } }$ //L'Hospital'sRule $\left( \frac { 0 }{ 0 } \right)$

$Res\left( f\left( { z }_{ k } \right) \right) =\frac { { e }^{ i\left( \frac { 2k+1 }{ 2n } \pi \right) } }{ 2n\cdot { e }^{ i\left( 2k+1 \right) \pi } } =\frac { { e }^{ i\frac { \pi }{ n } k }\cdot { e }^{ i\frac { \pi }{ 2n } } }{ 2n\cdot { e }^{ i2\pi k }\cdot { e }^{ i\pi } } =\frac { { \left( { e }^{ i\frac { \pi }{ n } } \right) }^{ k }\cdot { e }^{ i\frac { \pi }{ 2n } } }{ 2n\cdot { { \left( { e }^{ i2\pi } \right) }^{ k } }\cdot { e }^{ i\pi } }$ $//{ z }_{ k }={ e }^{ i\left( \frac { 2k+1 }{ 2n } \pi \right) }$ // Euler's Formula

$Res\left( f\left( { z }_{ k } \right) \right) =\frac { { -e }^{ i\frac { \pi }{ 2n } } }{ 2n } { \left( { e }^{ i\frac { \pi }{ n } } \right) }^{ k }$ $//{ e }^{ i2\pi }=1,{ e }^{ i\pi }=-1$

so $\sum _{ { z }_{ k }\in A }^{ }{ Res\left( f\left( { z }_{ k } \right) \right) } =\sum _{ k=0 }^{ n-1 }{ \frac { { -e }^{ i\frac { \pi }{ 2n } } }{ 2n } { \left( { e }^{ i\frac { \pi }{ n } } \right) }^{ k } } =\frac { { -e }^{ i\frac { \pi }{ 2n } } }{ 2n } \sum _{ k=0 }^{ n-1 }{ { \left( { e }^{ i\frac { \pi }{ n } } \right) }^{ k } } =\frac { { -e }^{ i\frac { \pi }{ 2n } } }{ 2n } \cdot \frac { { \left( { e }^{ i\frac { \pi }{ n } } \right) }^{ n }-1 }{ { e }^{ i\frac { \pi }{ n } }-1 }$ //geometric sum

$=\frac { { -e }^{ i\frac { \pi }{ 2n } } }{ 2n } \cdot \frac { { e }^{ i\pi }-1 }{ { e }^{ i\frac { \pi }{ n } }-1 } =\frac { { -e }^{ i\frac { \pi }{ 2n } } }{ 2n } \cdot \frac { -2 }{ { e }^{ i\frac { \pi }{ n } }-1 } \cdot \left( \frac { { e }^{ -i\frac { \pi }{ 2n } } }{ { e }^{ -i\frac { \pi }{ 2n } } } \right) =\frac { 2 }{ 2n\left( { e }^{ i\frac { \pi }{ 2n } }-{ e }^{ -i\frac { \pi }{ 2n } } \right) } \cdot \left( \frac { i }{ i } \right)$

$=\frac { 1 }{ i } \cdot \frac { 1 }{ 2n\sin { \left( \frac { \pi }{ 2n } \right) } } \quad //\sin { \left( x \right) } =\frac { { e }^{ x }-{ e }^{ -x } }{ 2i }$

Note(2) :

$\sin { \left( \frac { \pi }{ 8 } \right) } =\sin { \left( \frac { 1 }{ 2 } \cdot \frac { \pi }{ 4 } \right) } =\sqrt { \frac { 1-\cos { \left( \frac { \pi }{ 4 } \right) } }{ 2 } } =\sqrt { \frac { 1-\frac { \sqrt { 2 } }{ 2 } }{ 2 } }$

$=\sqrt { \frac { 2-\sqrt { 2 } }{ 4 } } =\frac { 1 }{ 2 } \cdot \sqrt { 2-\sqrt { 2 } }$