Integral Maximized

Let the integral be $I$ . Then

$\begin{aligned} I & = \int_a^{a+8} e^{-x}e^{-x^2} dx = \int_a^{a+8} e^{-(x^2+x)} dx = \int_a^{a+8} e^\frac 14 e^{-\left(x+\frac 12\right)^2} dx & \small \blue{\text{Let }u = x + \frac 12} \\ & = \sqrt[4]e \int_{a+0.5}^{a + 8.5} e^{-u^2} du \end{aligned}$

We note that the integrand $f(u) = e^{-u^2} > 0$ for all real $u$ and it is an even function with maximum at $u=0$ (see graph below.

To get the maximum value of integral or largest area under the curve, we position the interval $[a+0.5, a+8.5]$ evenly into two halves with $a + 0.5 = -4$ and $a+8.5 = 4$ or $a = \boxed{-4.5}$ .

Consider the function $f \colon \R \to \R$ defined by $f(a) = \int_a^{a+8} e^{-x-x^2} \mathrm{d} x \quad (a \in \R).$ In order to maximize the function $f$ we will find its critical points. By the Fundamental theorem of calculus function $f$ is differentiable and $f^{\prime}(a) = e^{-(a+8)-(a+8)^2}-e^{-a-a^2} \quad (a \in \R).$ Because the function $\R \ni s \to e^s \in \R$ is injective, we have that that $f^{\prime}(a) = 0$ if and only if $-(a+8)-(a+8)^2 = -a -a^2$ , which can be rewritten as $a = -4.5$ . Therefore $a_0 = -4.5$ is a critical point of the function $f$ .

Note, that the function $\R \ni x \to -x-x^2 \in \R$ is bounded from above, therefore, the function $f$ is bounded (we integrate over an interval of fixed length). Hence $f$ attains its maximum. We have shown, that it has to attain it at $a_0 = -4.5$ .

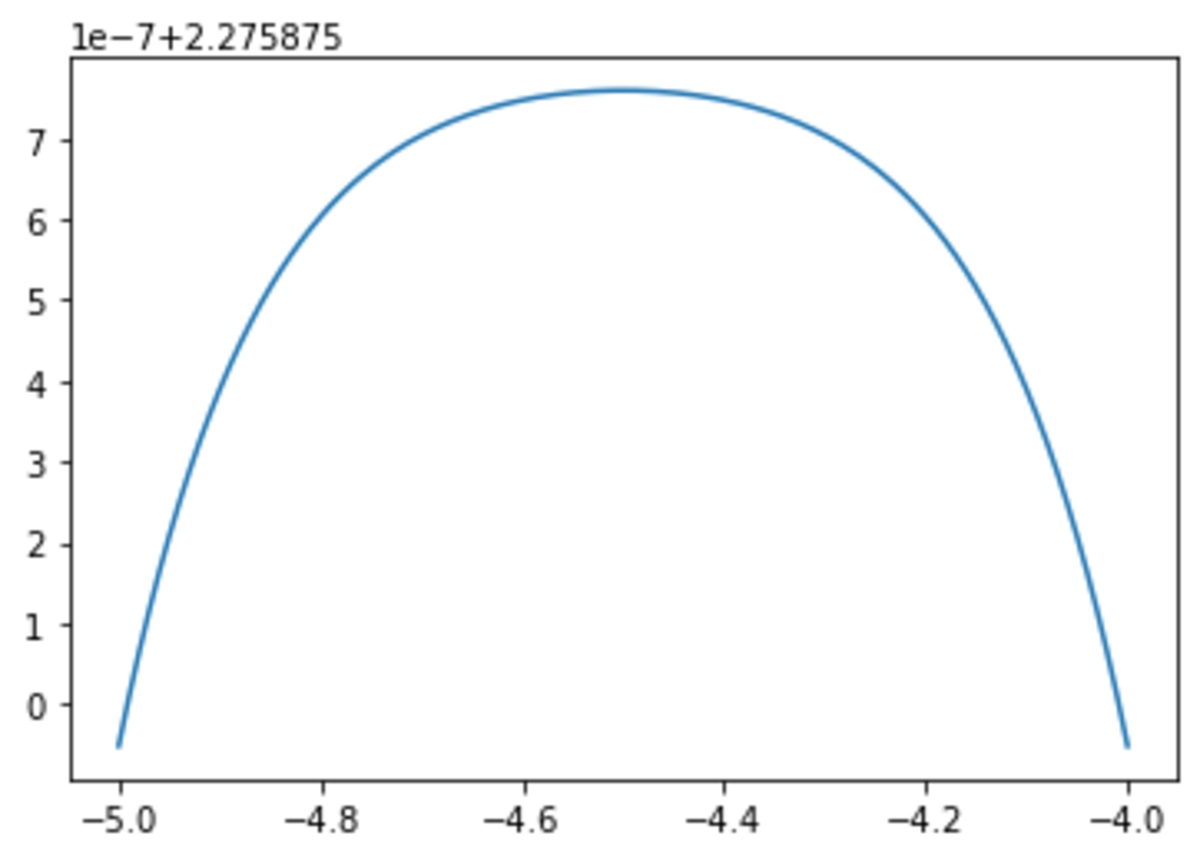
Side remark: on the plot below, you can see the graph of the function $f$ on the interval $[-5, -4]$ . Observe how slight the maximum of $f$ is.