Definite integral of mixtures of irrational numbers

$I =\large \int_0^1 \dfrac{\tan^{-1}x}{x^{2/3}} \, dx$ Integrating by parts we get,(with $\dfrac{1}{x^{2/3}}$ as the first function ) $\dfrac{3\pi}{4}-3\displaystyle\int_{0}^{1}\dfrac{x^{1/3}dx}{1+x^{2}}$ Now, write: $\dfrac{1}{1+x^{2}} = \displaystyle\sum_{n=0}^{\infty}(-1)^{n}x^{2n}$ So that: $I =\dfrac{3\pi}{4} -\dfrac{3}{2}\displaystyle\sum_{n=0}^{\infty}\dfrac{(-1)^{n}}{n+\frac{2}{3}}$ As, $\displaystyle\sum_{n=0}^{\infty}\dfrac{(-1)^{n}}{n+a/b} = \Psi(-1,1,\dfrac{a}{b} )$ where $\Psi(z,s,a)$ is the Hurwitz Lerch Transcendent So, $I = \pi \left[\dfrac{3}{4} -\dfrac{\sqrt{3}}{2}\right] +\dfrac{3}{2}\ln{2}$

Using the taylor series of $\tan^{-1}(x)$ we have :-

$\displaystyle \tan^{-1}(x) = \sum_{r=0}^{\infty}\frac{(-1)^{r}x^{2r+1}}{2r+1}$

So $\displaystyle \int_{0}^{1}\frac{\tan^{-1}(x)}{x^{\frac{2}{3}}}\,dx=\sum_{r=0}^{\infty}(-1)^{r}\frac{1}{(2r+1)(2r+\frac{4}{3})}=\sum_{r=0}^{\infty}(-1)^{r}\frac{3}{(2r+1)(6r+4)} =\sum_{r=0}^{\infty}(-1)^{r}\frac{3}{2\cdot (2r+1)(3r+2)}$

$\displaystyle = \frac{3}{2}\sum_{r=0}^{\infty}\frac{(-1)^{r}}{r+1}\left(\frac{1}{2r+1}-\frac{1}{3r+2}\right)$

$\displaystyle = \frac{3}{2}\sum_{r=0}^{\infty}\left(\frac{(-1)^{r}}{(2r+1)(r+1)} - \frac{(-1)^{r}}{(r+1)(3r+2)}\right)$

$\displaystyle = 3\sum_{r=0}^{\infty}\frac{(-1)^{r}}{(2r+2)(2r+1)} - \frac{9}{2}\sum_{r=0}^{\infty}\frac{(-1)^{r}}{(3r+3)(3r+2)}$

$\displaystyle = 3\sum_{r=0}^{\infty}\left(\frac{(-1)^{r}}{2r+1} - \frac{(-1)^{r}}{2r+2}\right) - \frac{9}{2}\sum_{r=0}^{\infty}\left(\frac{(-1)^{r}}{3r+2}-\frac{(-1)^{r}}{3r+3}\right)$

Now we know the taylor series $\displaystyle \frac{1}{1+x} = \sum_{r=0}^{\infty}(-1)^{r}x^{r}$ . So in this series....replacing $x$ by $x^{2}$ or $x^{3}$ as required and multiplying by $x$ or $x^{2}$ in the numerator as required and then integrating from $0$ to $1$ we would get the appropriate summations.

For example :-

$\displaystyle \int_{0}^{1}\frac{1}{1+x^{2}}\,dx = \sum_{r=0}^{\infty}\frac{(-1)^{r}}{2r+1}\,\,\,\,\,\,\text{and}\,\,\,\,\, \int_{0}^{1}\frac{x}{1+x^{2}}\,dx=\sum_{r=0}^{\infty}\frac{(-1)^{r}}{2r+2}$ and so on.....

So we have :-

$\displaystyle 3\int_{0}^{1}\left(\frac{1}{1+x^{2}}-\frac{x}{1+x^{2}}\right)\,dx - \frac{9}{2}\int_{0}^{1}\left(\frac{x}{1+x^{3}}-\frac{x^{2}}{1+x^{3}}\right)\,dx$

Essentially what we did was we converted the integral into a series form and then rearranged some terms and then again reconverted it to an integral but this time it is an integral of rational algebraic functions.

Now each of these integrals posses an antiderivative and are quite easy to figure out. Let me provide the hints one by one:-

$\displaystyle \frac{1}{1+x^{2}}$ :- Standard $\text{arctan}$ form.

$\displaystyle \frac{x}{1+x^{2}}$ :- substitute $x^{2}=t$

$\displaystyle \frac{x}{1+x^{3}} = \frac{x+1}{1+x^{3}} - \frac{1}{1+x^{3}} = \frac{1}{1-x+x^{2}} - \frac{1}{1+x^{3}}$ :- The first one can be made into the arctan format by some rearrangements and the second one can be solved using partial fractions. Here is a video showing this .

$\displaystyle \frac{x^{2}}{1+x^{3}}$ :- Substitute $x^{3} = u$ .

So after solving all of these integrals we get our answer as:-

$\displaystyle \pi\left(\frac{3}{4}-\frac{\sqrt{3}}{2}\right) + \frac{3}{2}\ln(2)$ .

I did not show any working regarding the integral. I used desmos to calculate my integral and the integral in question and it gave the same value proving that my method is correct. Here is a picture:-

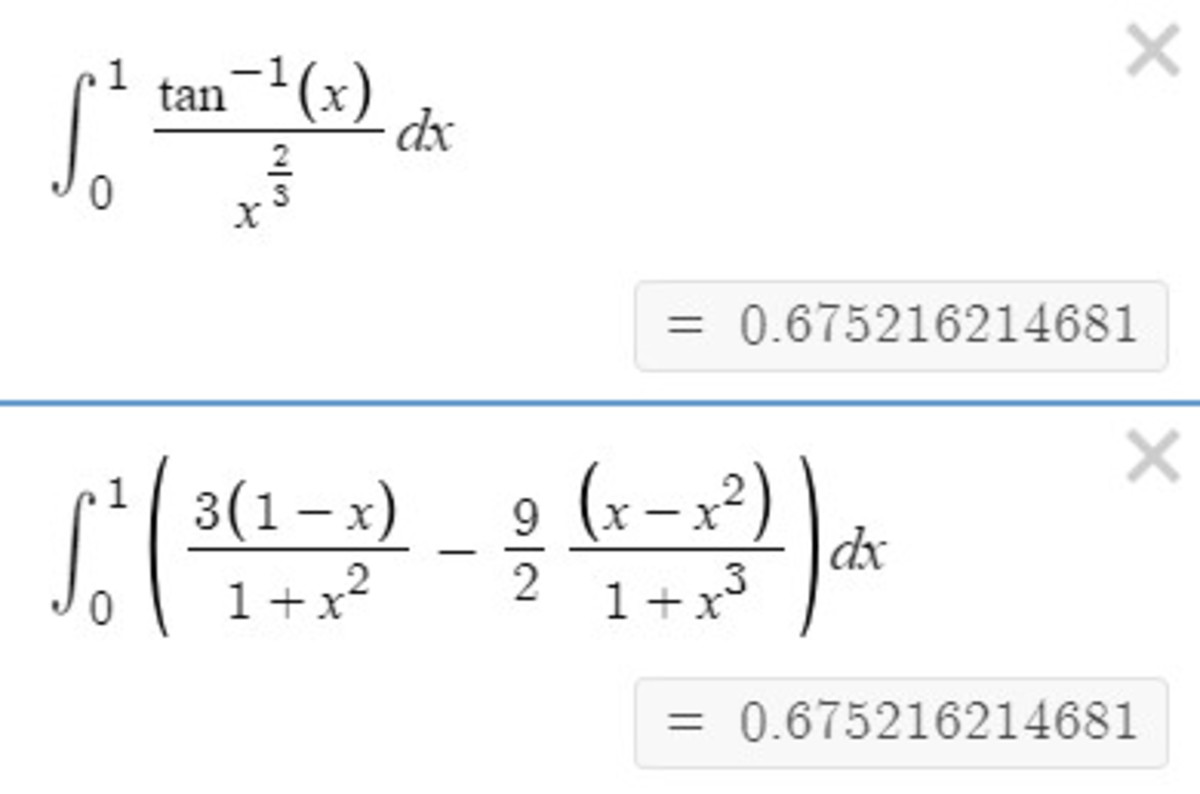
Complete solution is not here.