Integration of Weird Functions - 3

Using substitution x=10-x and y=10-y:

$I=\int_{0}^{10}\int_{0}^{10} \lfloor{x+y}\rfloor dxdy = \int_{0}^{10}\int_{0}^{10} \lfloor{10-x+10-y}\rfloor dxdy$

Add two copies of integral and move all under one integral sign:

$2I=\int_{0}^{10}\int_{0}^{10} \lfloor{x+y}\rfloor + \lfloor{20-x-y}\rfloor dxdy$

If x+y is not integer then $\lfloor{x+y}\rfloor + \lfloor{20-x-y}\rfloor = 19$

x+y is integer on area size 0, so $2I=\int_{0}^{10}\int_{0}^{10} 19 dxdy = 1900$

So $I=950$

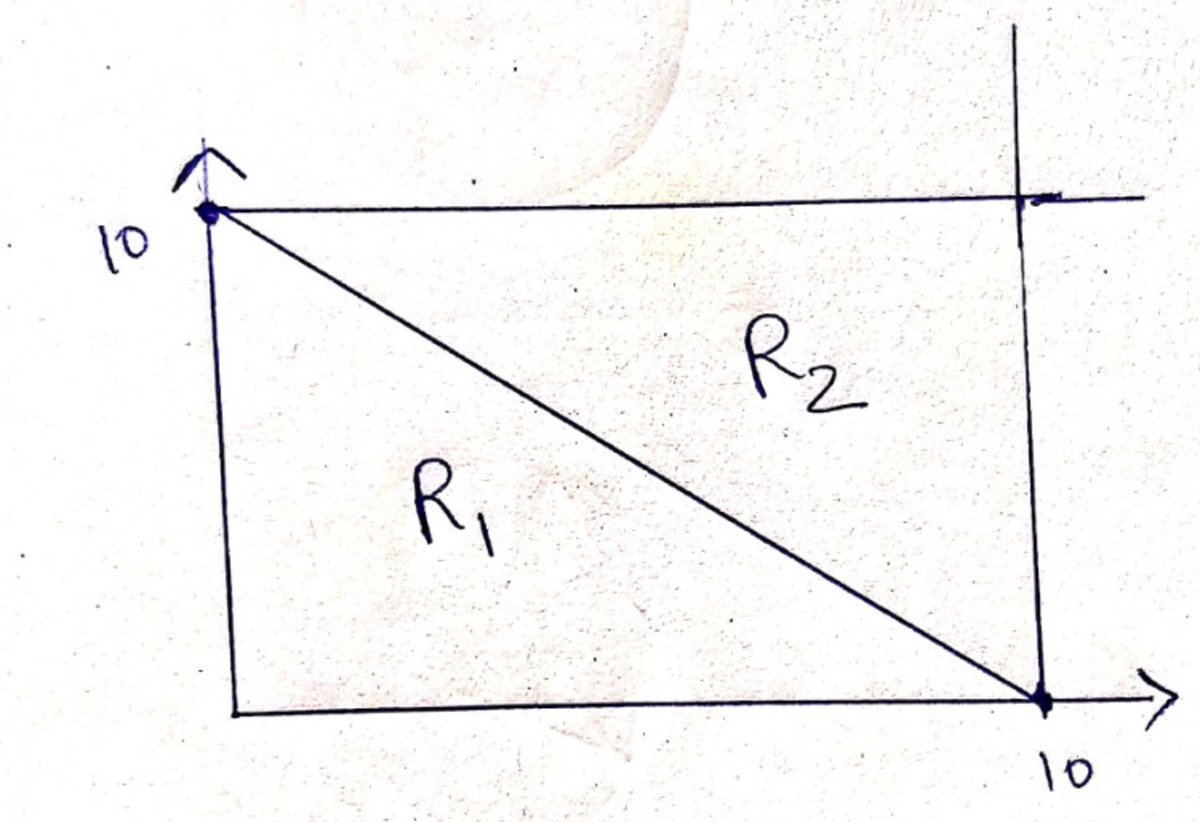
Let us divide the square formed by $x=0,x=10,y=0,y=10$ into two regions $R_{1}$ and $R_{2}$

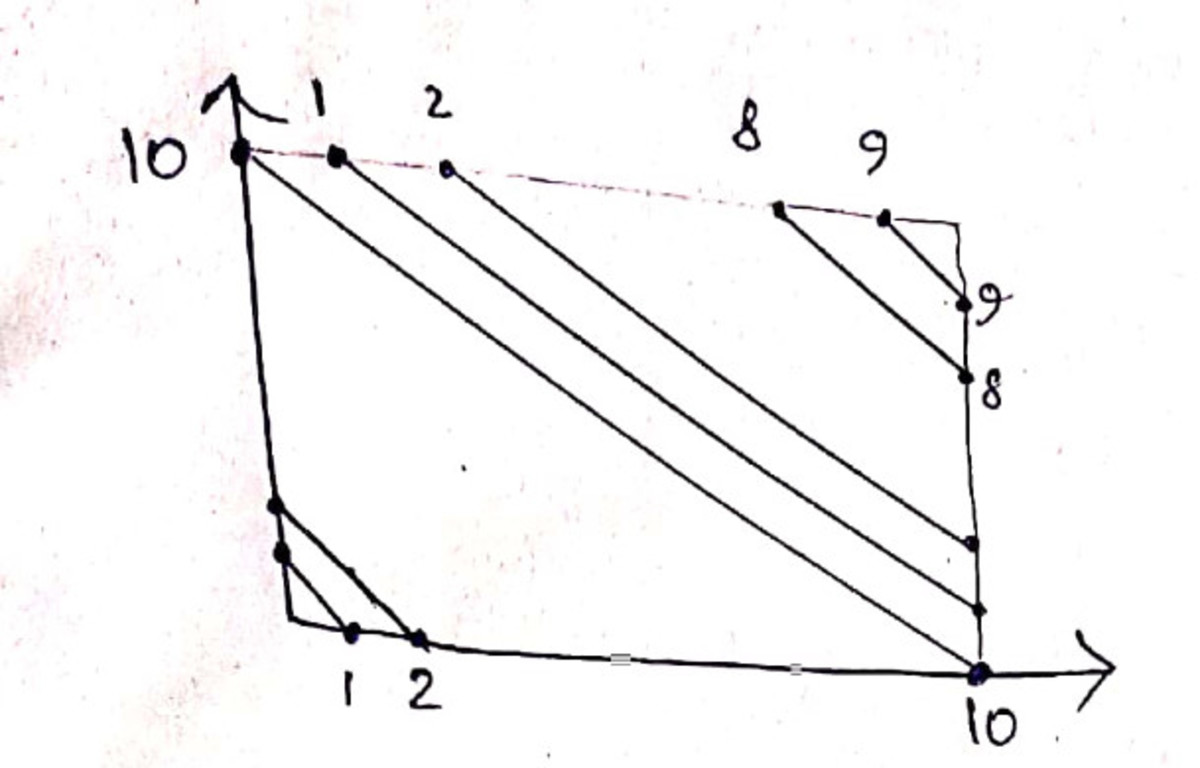
Now let us draw the lines $x+y=1 , \,\, x+y =2 ,\,\, x+y=3,\,\, ........x+y=19$

Now let's think of a vital concept. Double integral over a region of a constant function is just equal to the constant times the area of the region .

We know that $\displaystyle r\leq x+y < r+1 \implies \lfloor x+y \rfloor = r$ .

So if we denote the region $r\leq x+y < r+1$ which lies inside the square as $T_{r}$ . Then the double integral of the function over this region is just equal to :-

$\displaystyle r \cdot Area\,\, of\,\,T_{r}$ .

Now area of $T_{r}$ can be written as the difference of areas of two triangles.

Now consider the region $R_{1}$

Here the area of $T_{r}$ is given by the difference of areas of triangles formed by the lines $x+y=r+1,\,x=0,\,y=0$ and the lines $x+y=r,\,x=0,\,y=0$ Which is given by $\displaystyle \frac{(r+1)^{2} - r^{2}}{2}$ .

Hence the double integral in that region $T_{r}$ is equal to $\displaystyle \frac{r\left((r+1)^{2}-r^{2}\right)}{2}$

So $\displaystyle \iint_{R_{1}}\lfloor x+y \rfloor dxdy = \sum_{r=0}^{r=9}r\cdot Area\,\,of\,\,T_{r} =\sum_{r=0}^{9} \frac{r\left((r+1)^{2}-r^{2}\right)}{2}$

In $R_{2}$ we just have to use symmetry . There the double integral would be :-

$\displaystyle \iint_{R_{2}}\lfloor x+y \rfloor dxdy = \frac{10}{2}\cdot (10^{2}-9^{2}) + \frac{11}{2}\cdot (9^{2}-8^{2}) +.............+\frac{18}{2}\cdot (2^{2}-1^{2}) + \frac{19}{2}\cdot (1^{2}-0^{2})$

$\displaystyle = \sum_{r=0}^{9} (19-r)\frac{\left((r+1)^{2}-r^{2}\right)}{2}$ .

So the in total $\displaystyle \iint_{R_{1}}\lfloor x+y \rfloor dxdy + \iint_{R_{2}}\lfloor x+y \rfloor dxdy = \int_{0}^{10}\int_{0}^{10}\lfloor x+y \rfloor dxdy=\sum_{r=0}^{9}19\cdot\frac{\left((r+1)^{2}-r^{2}\right)}{2}=\sum_{r=0}^{9}19\cdot \frac{2r+1}{2}=950$

Consider $I_n$ as follows:

$\begin{aligned} I_n & = \int_0^n \int_0^n \lfloor \blue x + \red y \rfloor \ dx\ dy \\ & = \int_0^n \int_0^n \lfloor \blue{\lfloor x \rfloor + \{x\}} + \red{\lfloor y \rfloor + \{y\}} \rfloor \ dx\ dy \\ & = \int_0^n \int_0^n \left(\lfloor x \rfloor + \lfloor y \rfloor + \lfloor \{x\} + \{y\} \rfloor \right) dx\ dy \\ & = \int_0^n \int_0^n \left(\blue{\int_0^n \lfloor x \rfloor \ dx} + \int_0^n \lfloor y \rfloor \ dx + \red{\int_0^n \lfloor \{x\} + \{y\} \rfloor \ dx} \right) \ dy \\ & = \int_0^n \left(\blue{\sum_{k=1}^{n-1} k} + \lfloor y \rfloor x \ \bigg|_0^n + \red{n \int_{1-\{y\}}^1 dx} \right) dy \\ & = \int_0^n \left(\frac {n(n-1)}2 + n \lfloor y \rfloor + n \{y\} \right) dy \\ & = \frac {n(n-1)}2 \cdot y \ \bigg|_0^n + n \sum_{k=1}^{n-1} k + n^2 \int_0^1 y \ dy \\ & = \frac {n^2(n-1)}2 + \frac {n^2(n-1)}2 + \frac {n^2}2 \\ & = \frac {n^2(2n-1)}2 \end{aligned}$

For $n=10$ , $I_{10} = \dfrac {100\cdot 19}2 = \boxed{950}$ .