Integral to the Maximum

$I=\int _{ 0 }^{ 2n\pi }{ max(sin\quad x,\quad { sin }^{ -1 }(sin\quad x))dx }$

$=n\left[ \int _{ 0 }^{ \frac { \pi }{ 2 } }{ x\quad dx\quad +\quad \int _{ \frac { \pi }{ 2 } }^{ \pi }{ (\pi \quad -\quad x)dx\quad +\quad \int _{ \pi }^{ 2\pi }{ (sin\quad x)dx } } } \right]$

$=n\left[ \frac { { \pi }^{ 2 } }{ 8 } +\frac { { \pi }^{ 2 } }{ 2 } -\frac { 1 }{ 2 } \left( { \pi }^{ 2 }-\frac { { \pi }^{ 2 } }{ 4 } \right) -2 \right]$

$=n\left[ \frac { { \pi }^{ 2 } }{ 8 } +\frac { { \pi }^{ 2 } }{ 2 } -\frac { { 3\pi }^{ 2 } }{ 8 } -2 \right]$

$=\boxed{\frac{n(\pi^{2} - 8)}{4}}$

Same method with Harshvardhan Mehta better graph and maybe simpler calculations.

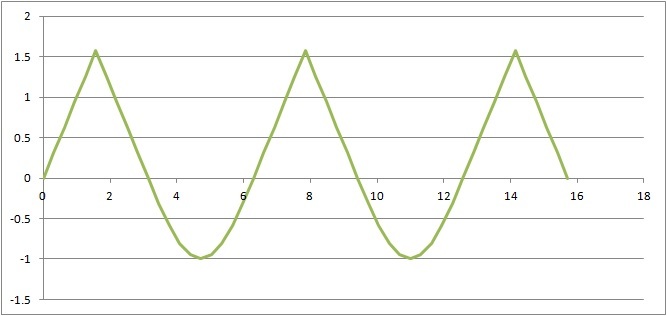
We note that for each cycle $(2\pi)$ , there is a positive triangle and a negative sine curve. Therefore,

$\begin{aligned} \displaystyle \int_0^{2n\pi} {\max {\left( \sin{x}, \sin^{-1} {(\sin{x})}\right)} dx} & = n \left( 2 \displaystyle \int_0^{\frac{\pi}{2}} {xdx} - 2 \int_0^{\frac{\pi}{2}} {\sin{x}dx} \right) \\ & = 2n \left( \left[ \frac {1}{2} x^2 \right]_0^{\frac{\pi}{2}} + \left[ \cos {x} \right]_0^{\frac{\pi}{2}} \right) \\ & = 2n \left( \frac {\pi^2}{8} - 1 \right) = \boxed {\dfrac{n(\pi^2-8)}{4}} \end{aligned}$