Integral with the floor function
Which of the following ranges does the area of all closed regions bounded by the x -axis , all lines of the form x = k where k ∈ N , and y = 1 − x ⌊ x ⌋ fall in?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
A quicker way of reaching the conclusion is that when { x } > 2 1 , then we have 1 − x ⌊ x ⌋ = x x − ⌊ x ⌋ = x { x } > 2 x 1 > 2 ( ⌊ x ⌋ + 1 ) 1 .
Hence, ∫ 1 − x ⌊ x ⌋ d x > 2 1 ( 2 1 + 3 1 + 4 1 + … ) .
Log in to reply
My solution's idea was obtained from graphing the function and seeing that it's composed of several (countably infinitely many) curves from ( k , 0 ) to ( k + 1 , k + 1 1 ) for all positive integer k , and that all the curves are concave. I "smoothen" each curve to just a single line from ( k , 0 ) to ( k + 1 , k + 1 1 ) , where since the curve was concave, won't increase the area under it.
Plot shamelessly copied from WolframAlpha and then modified with MS Paint. Original curve in blue, modified curve in red:
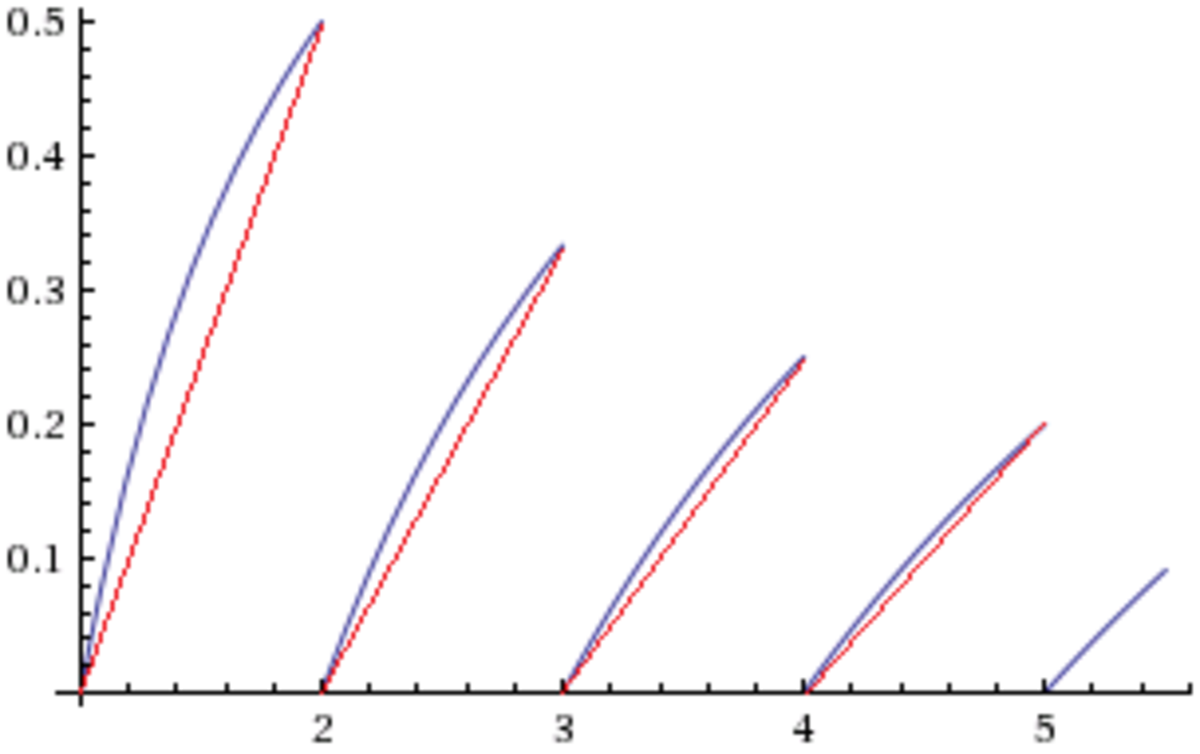
Excellent solution, @Ivan Koswara !
Observe that 1 − x ⌊ x ⌋ = x x − ⌊ x ⌋ > ⌊ x ⌋ + 1 x − ⌊ x ⌋ for all x ≥ 1 , since x < ⌊ x ⌋ + 1 for all x .
The sought area is ∫ 1 ∞ x x − ⌊ x ⌋ d x . Due to the above observation, this is greater than ∫ 1 ∞ ⌊ x ⌋ + 1 x − ⌊ x ⌋ d x . Break this integral on unit intervals:
∫ 1 ∞ ⌊ x ⌋ + 1 x − ⌊ x ⌋ d x
= k = 1 ∑ ∞ ∫ k k + 1 ⌊ x ⌋ + 1 x − ⌊ x ⌋ d x
Since k is an integer, for k ≤ x < k + 1 we haave ⌊ x ⌋ = k , so we can simplify the integral further:
= k = 1 ∑ ∞ ∫ k k + 1 k + 1 x − k d x
= k = 1 ∑ ∞ k + 1 2 1 x 2 − k x ∣ ∣ ∣ ∣ x = k k + 1
= k = 1 ∑ ∞ k + 1 2 1 ( k + 1 ) 2 − k ( k + 1 ) − k + 1 2 1 k 2 − k 2
= k = 1 ∑ ∞ k + 1 2 1 ( 2 k + 1 ) − k
= k = 1 ∑ ∞ 2 ( k + 1 ) 1
= 2 1 ⋅ k = 2 ∑ ∞ k 1
But the latter factor is infinite: it is the divergent series ∑ k = 1 ∞ k 1 , subtracted by the finite quantity 1 1 . Multiplying by a positive constant 2 1 leaves it infinity.
Our integral is greater than this result, but this result is infinity, so our integral must be infinity itself.