Can we cancel them out?

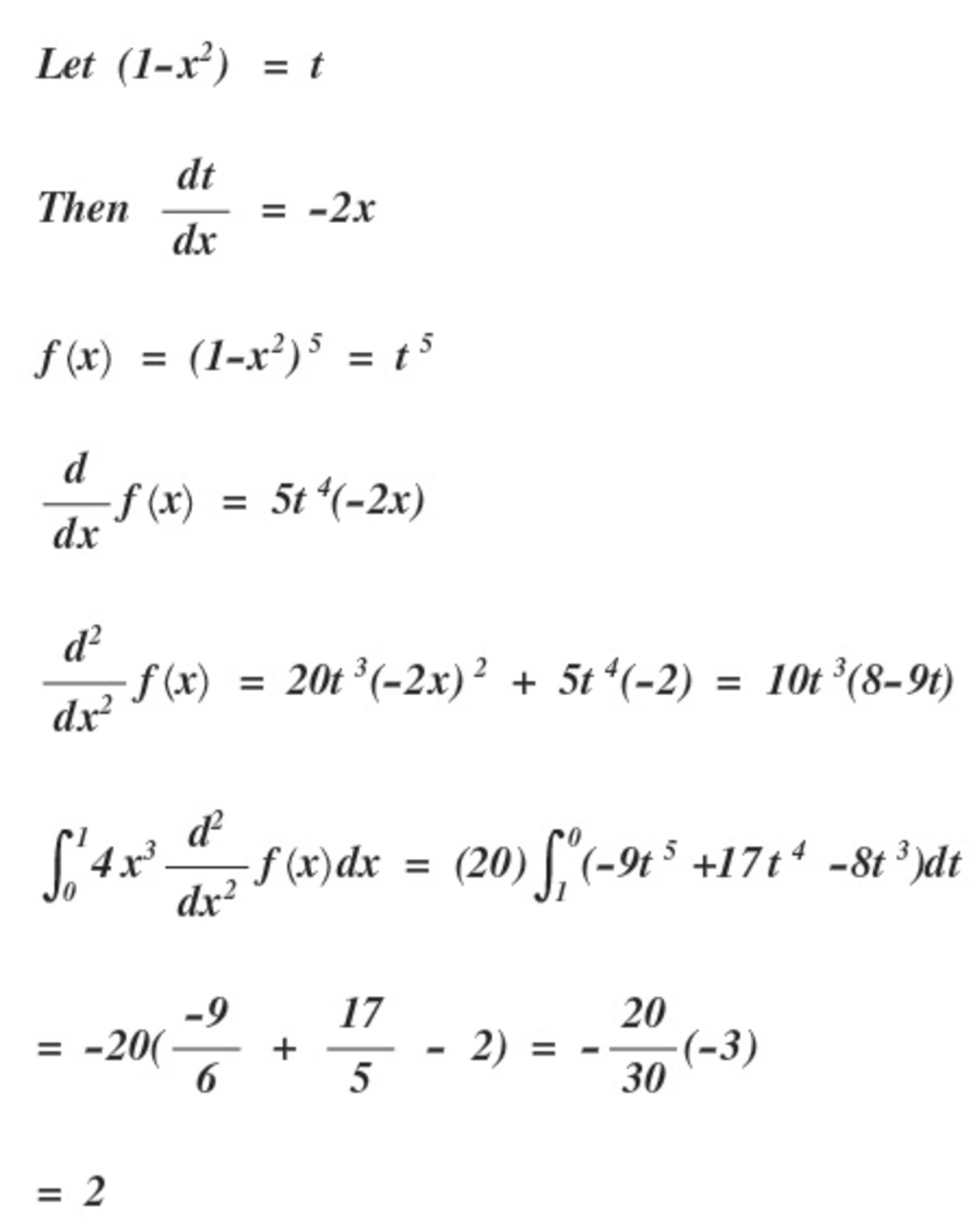
We want to get reduce the order of the derivative (or get rid of it completely) so this hints at the fact that integration by parts may be useful and possibly integration by substitution.

$\ I = \int_{0}^{1} 4x^3 ( \frac{d^2}{dx^2}(1-x^2)^5 ) dx$ $\ = [4x^3 ( \frac{d}{dx}(1-x^2)^5 )]_0^1 -\int_{0}^{1} 12x^2 ( \frac{d}{dx}(1-x^2)^5 ) dx$ $\ = -12 \int_{0}^{1} x^2 ( \frac{d}{dx}(1-x^2)^5 ) dx$ because the derivative of $\ (1-x^2)^k$ ( $\ k \ne -1$ ) will have a factor of $\ (1-x^2)$ which will equal zero when x = 1 and $\ 4x^3$ will equal zero when x = 0. Now let $\ S = \int_{0}^{1} x^2 ( \frac{d}{dx}(1-x^2)^5 ) dx$ : $\ S = [x^2(1-x^2)^5]_0^1 - \int_{0}^{1} 2x(1-x^2)^5 dx$ $\ = - \int_{0}^{1} 2x(1-x^2)^5 dx$ Now let $\ u = x^2$ and use integration by substitution (and inspection): $\ S = -\int_{0}^{1} (1-u)^5 = [\frac{1}{6} (1-u)^6]_0^1 = -\frac{1}{6}$ $\therefore\ I = -12S = \boxed{2}$

$\displaystyle \int_0^1 4x^3\left(\frac{d^2}{dx^2} \left(1-x^2 \right)^5 \right) dx \\ = \displaystyle \int_0^1 4x^3\left(\frac{d^2}{dx^2} \left(1 - 5x^2 + 10x^4 - 10x^6 + 5x^8 - x^{10} \right) \right) \\ = \displaystyle \int_0^1 4x^3 \left( \frac {d} {dx} \left(- 10x + 40x^3 - 60x^5 + 40x^7 - 10x^9 \right) \right) \\ = \displaystyle \int_0^1 4x^3 \left( - 10 + 120x^2 - 300x^4 + 280x^6 - 90x^8 \right) dx \\ = \displaystyle \int _0 ^1 \left( - 40x^3 + 480x^5 - 1200x^7 + 1120 x^9 - 360x^{11} \right) \\ = \displaystyle \left[ - \frac{40x^4}{4} + \frac{480x^6}{6} - \frac{ 1200 x^8}{8} + \frac{1120 x^{10}}{10} - \frac{360x^{12}}{12} \right]_0^1 \\ = \displaystyle \left[ - 10x^4 + 80x^6 - 150 x^8 + 112 x^{10} - 30 x^{12} \right]_0^1 \\ = - 10 + 80 - 150 + 112 - 30 \\ = \boxed{2}$

$\displaystyle \int_{0}^{1} 4x^{3}(\frac{d^{2}}{dx^{2}}(1-x^{2})^{5})dx$ $= (4x^{3}(\frac{d}{dx}(1-x^{2})^{5}]_{0}^{1} - \displaystyle \int_{0}^{1} 12x^{2}(\frac{d}{dx}(1-x^{2})^{5})dx$ $=\displaystyle \int_{0}^{1}24(1-x^{2})^{5}dx$ We let $x^{2}=u => dx = \frac{du}{2x}$ . Therefore $\displaystyle \int_{0}^{1}12(1-u)^{5}du$ $(-2(1-u)^{6}]_{0}^{1} = 2$

The integral of (-40 x^3 (x^2-1)^3 (9 x^2-1)) dx from 0 to 1 = 2. If you cannot take the second derivative in your head, the make a change of variable and arrive at the same answer after a little more time.