Integrate this one!
∫ 0 ∞ ( x 2 + 4 ) 3 ( 1 2 − x 2 ) cos ( 2 x ) d x = C e D A π B
where A , B , C , D are integers and A , C being coprime.
Find A + B + C + D
The answer is 34.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
That's awesome!!!!!!
I approached it in a non-complex analysis way......namely by Feynmann Technique of Differentiation under the integral sign.


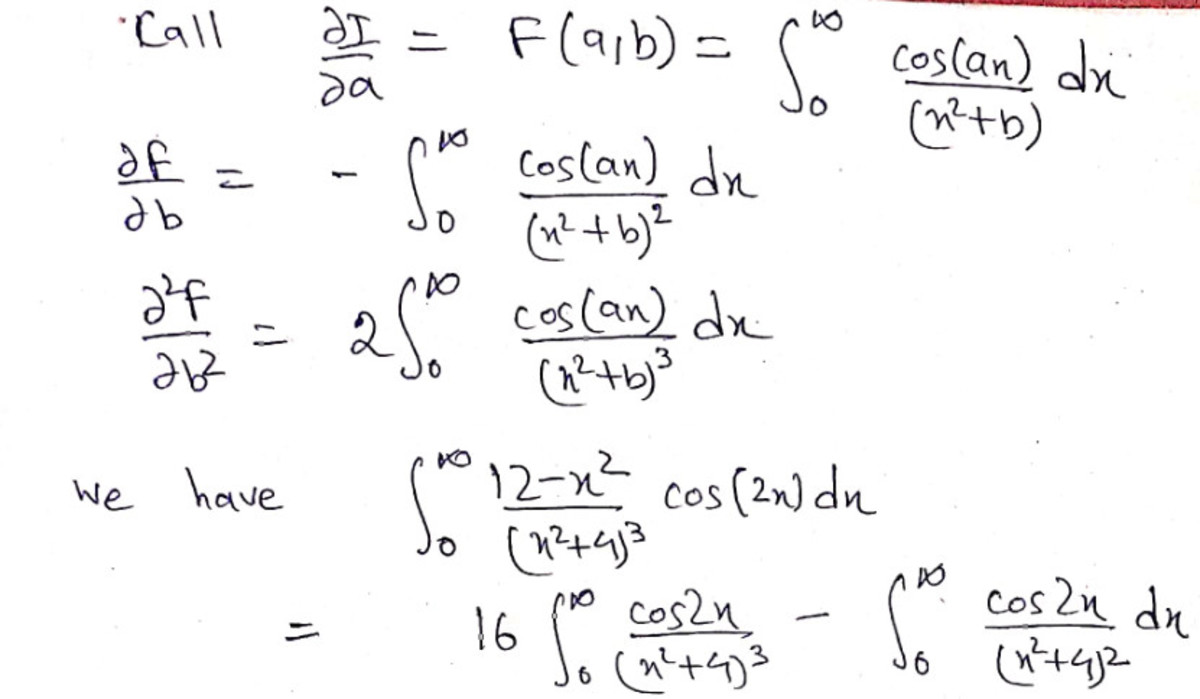
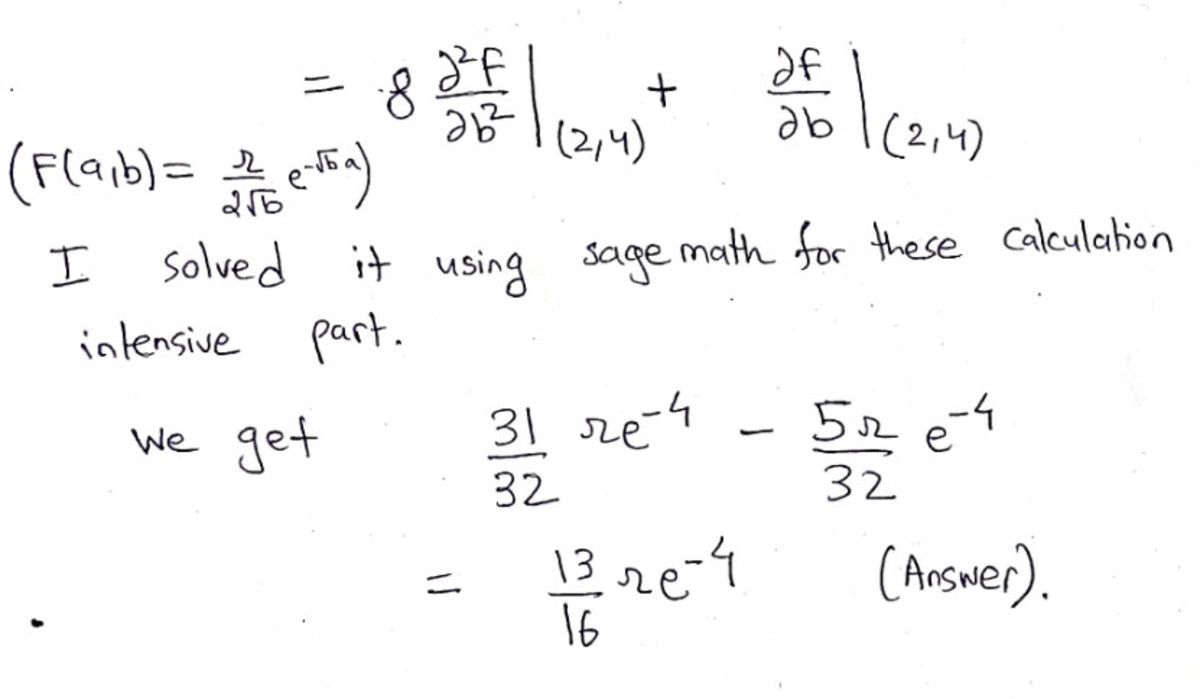

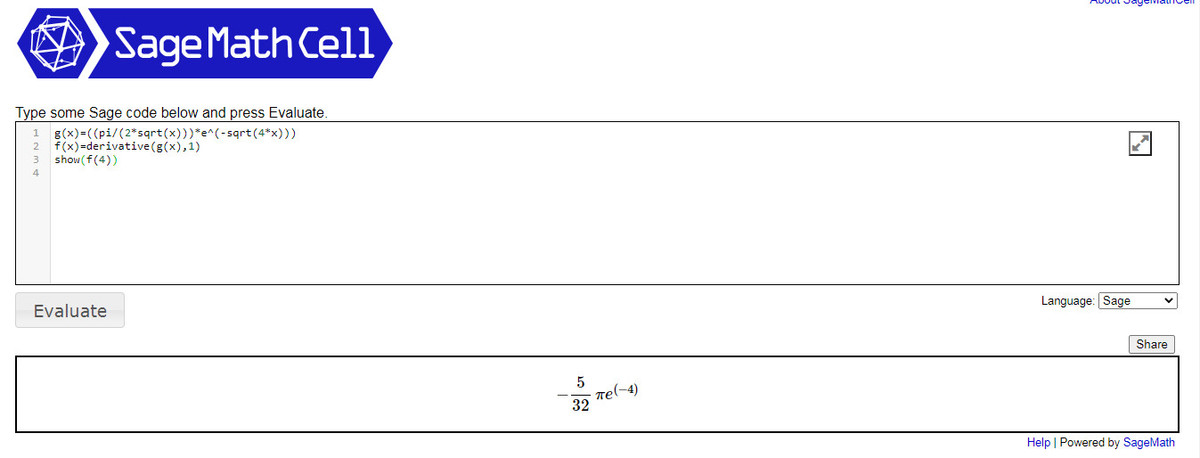
Now I skipped the solution of the 2nd order linear oridinary differential equation in terms of a with constant coefficients as it is very easy and I solved it using the operator method using auxiliary equations and finding complementary functions and particular integrals. You can find these in any differential equation books.
As for my initial assumed function:- I was inspired by a problem shown on Flammable Maths youtube channel . Here is the link to it Flammable Maths video .
I am very sorry that I did not latex it out . Maybe someday I will.
∫ 0 ∞ ( x 2 + 4 ) 3 ( 1 2 − x 2 ) cos ( 2 x ) d x = I 1 1 2 ∫ 0 ∞ ( x 2 + 4 ) 3 cos ( 2 x ) d x − I 2 ∫ 0 ∞ ( x 2 + 4 ) 3 x 2 cos ( 2 x ) d x
Consider f ( z ) = ( z 2 + 4 ) 3 e i 2 z .
Draw a simple closed curve C about the origin on the complex plane as shown below (in the anticlockwise direction):
Using the Cauchy-integral formula, the contour integral of f ( z ) can be given by
∮ C f ( z ) d z = ∫ − R R f ( z ) d z + ∫ γ R f ( z ) d z ⟹ ∫ − R R f ( z ) d z = ∮ C f ( z ) d z − ∫ γ R f ( z ) d z
where R > 2 .
Now, ( z 2 + 4 ) 3 = 0 ⟹ ( z + 2 i ) ( z − 2 i ) = 0 .
Thus f ( z ) has poles at z = 2 i and z = − 2 i out of which only z = 2 i lies inside our contour (as visible from the diagram above).
Since C is a positively oriented simple closed curve applying the Cauchy's residue theorem, we have
∮ C f ( z ) d z = 2 π i ∑ Res ( f ( z ) , 2 i )
where the sum of residues is simply just one residue.
Res ( f ( z ) , 2 i ) = 2 ! 1 z → 2 i lim d z 2 d 2 [ ( z − 2 i ) 3 f ( z ) ] = 2 1 z → 2 i lim d z 2 d 2 [ ( z 2 + 4 ) 3 ( z − 2 i ) 3 e i 2 z ] = 2 1 z → 2 i lim d z 2 d 2 [ ( z + 2 i ) 3 e i 2 z ] = 2 1 z → 2 i lim ( z + 2 i ) 5 − 4 e i 2 z ( z 2 + 7 i z − 1 3 ) = 5 1 2 i 3 1 e − 4 = 5 1 2 i e 4 3 1
Thus
∮ C f ( z ) d z = 2 π i ( 5 1 2 i e 4 3 1 ) = 2 5 6 e 4 3 1 π
Using estimation lemma
∣ ∣ ∣ ∣ ∫ γ R f ( z ) d z ∣ ∣ ∣ ∣ ≤ length ( γ R ) × max ∣ f ( z ) ∣
Where length ( γ R ) = π R and max ∣ f ( z ) ∣ = ( R 2 − 4 ) 3 1 (I'll leave it upto the reader to compute these).
So
∣ ∣ ∣ ∣ ∫ γ R f ( z ) d z ∣ ∣ ∣ ∣ ≤ ( R 2 − 4 ) 3 π R → 0 as R → ∞
Thus, we have evaluated the real part of f ( z ) by this method. Hence
∮ C f ( z ) d z = ∫ − R R f ( z ) d z ⟹ 2 5 6 e 4 3 1 π = ∫ − ∞ ∞ ( x 2 + 4 ) 3 cos ( 2 x ) d x As R ( e i 2 x ) = cos ( 2 x ) ⟹ 2 5 6 e 4 3 1 π = 2 ∫ 0 ∞ ( x 2 + 4 ) 3 cos ( 2 x ) d x even function ⟹ ∫ 0 ∞ ( x 2 + 4 ) 3 cos ( 2 x ) d x = 5 1 2 e 4 3 1 π
Hence
I 1 = 1 2 ⋅ 5 1 2 e 4 3 1 π = 1 2 8 e 4 9 3 π
Consider the similar process but with f ( z ) = ( z 2 + 4 ) 3 z 2 e i 2 z .
This also has poles at z = 2 i and z = − 2 i out of which only z = 2 i lies inside the contour.
For residue
Res ( f ( z ) , 2 i ) = 2 ! 1 z → 2 i lim d z 2 d 2 [ ( z − 2 i ) 3 f ( z ) ] = 2 1 z → 2 i lim d z 2 d 2 [ ( z 2 + 4 ) 3 z 2 ( z − 2 i ) 3 e i 2 z ] = 2 1 z → 2 i lim d z 2 d 2 [ ( z + 2 i ) 3 z 2 e i 2 z ] = 2 1 z → 2 i lim ( z + 2 i ) 5 − 2 e i 2 z ( 2 z 4 + 1 0 i z 3 − 5 z 2 + 2 4 i z + 4 ) = 2 1 ⋅ 6 4 e 4 1 1 i = 1 2 8 e 4 1 1 i
Thus
∮ C f ( z ) d z = 2 π i ( 1 2 8 e 4 1 1 i ) = − 6 4 e 4 1 1 π
By estimation lemma, again we have
∣ ∣ ∣ ∣ ∫ γ R f ( z ) d z ∣ ∣ ∣ ∣ ≤ length ( γ R ) × max ∣ f ( z ) ∣
Here length ( γ R ) = π R and max ∣ f ( z ) ∣ = ( R 2 − 4 ) 3 R 2 .
So
∣ ∣ ∣ ∣ ∫ γ R f ( z ) d z ∣ ∣ ∣ ∣ ≤ ( R 2 − 4 ) 3 π R 3 → 0 as R → ∞
Thus, we have evaluated the real part of f ( z ) by this method. Hence
∮ C f ( z ) d z = ∫ − R R f ( z ) d z ⟹ − 6 4 e 4 1 1 π = ∫ − ∞ ∞ ( x 2 + 4 ) 3 x 2 cos ( 2 x ) d x As R ( e i 2 x ) = cos ( 2 x ) ⟹ − 6 4 e 4 1 1 π = 2 ∫ 0 ∞ ( x 2 + 4 ) 3 x 2 cos ( 2 x ) d x even function ⟹ ∫ 0 ∞ ( x 2 + 4 ) 3 x 2 cos ( 2 x ) d x = − 1 2 8 e 4 1 1 π
Hence
I 2 = − 1 2 8 e 4 1 1 π
Which gives
I 1 − I 2 = 1 2 8 e 4 9 3 π − ( − 1 2 8 e 4 1 1 π ) = 1 2 8 e 4 9 3 π + 1 2 8 e 4 1 1 π = 1 6 e 4 1 3 π
where A + B + C + D = 1 3 + 1 + 1 6 + 4 = 3 4 .