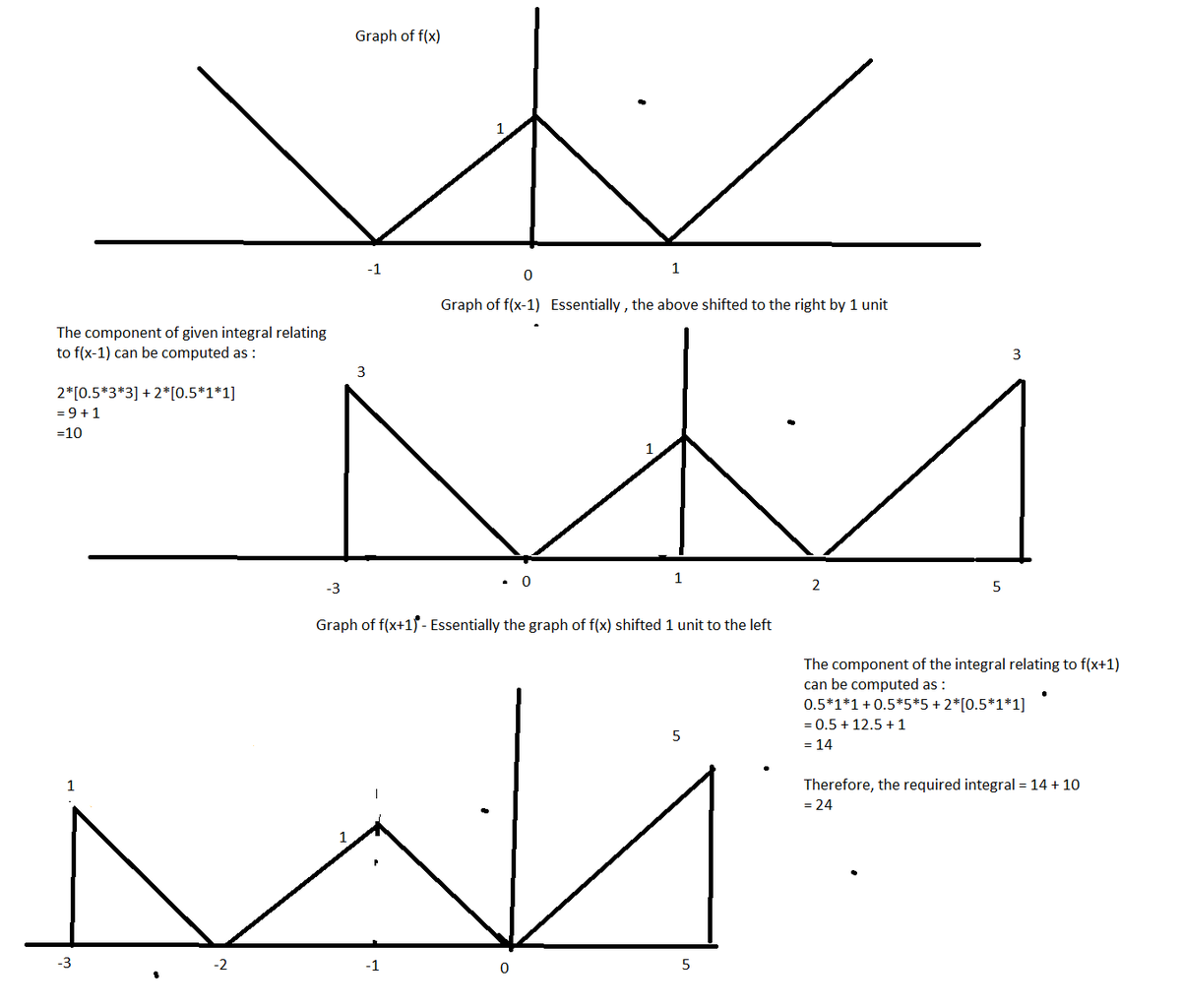
Integrating Over Absolute Values

$f(x)$ actually has a more compact form: $f(x) = ||x|-1|$ $g(x) = ||x-1|-1| + ||x+1|-1|$ This makes the integral easier conceptually. You can graph $g(x)$ and find the area of the region under it simply by dividing it into triangles and rectangles.

There is also a closed form for the indefinite integral, but as usual with absolute value functions, it is not compact at all and makes heavy use of the $\text{sgn}$ function.

$\int _{ -3 }^{ 5 }{ g(x) } dx=\int _{ -3 }^{ 5 }{ \{ f(x-1)+f(x+1)\} } dx=\int _{ -3 }^{ 5 }{ f(x-1) } dx+\int _{ -3 }^{ 5 }{ f(x+1) } dx\\ =\int _{ -4 }^{ 4 }{ f(x) } dx+\int _{ -2 }^{ 6 }{ f(x) } dx=14+10=24$

I approached this in a shamelessly numerical way.

$\begin{array}{ccc} x&f(x)&g(x)\\ -4 & 3 & {}\\ -3 & 2 & 4 \\ -2 & 1 & 2\\-1&0&2\\0&1&0\\1&0&2\\2&1&2\\3&2&4\\4&3&6\\5&4&8\\6&5&{} \end{array}$

(Use the definition to work out the f(x) column first and then the g(x) values are found easily by adding the previous and the following values of f(x))

Between any two integers g(x) is a linear function, and it can be integrated $exactly$ by the trapezium rule to find the area

$\dfrac{1}{2}(4+2(2+2+0+2+2+4+6)+8)=\boxed{24}$