Integration #7 (Corrected)

Rewrite the expression as $x^2 - y^2 = x^3 + xy^2$ . Then do the substitution (polar coordinates) $x = r \cos \theta, y = r \sin \theta$ . This turns the expression into $r^2 (\cos^2 \theta - \sin^2 \theta) = r^3 ( \cos^3 \theta + \cos \theta \sin^2 \theta) \implies \cos^2 \theta - \sin^2 \theta = r \cos \theta ( \cos^2 \theta + \sin^2 \theta ) \implies r \cos \theta = \cos^2 \theta - \sin^2 \theta \implies r = \cos \theta - \sin \theta \tan \theta$ . Here is a graph of the shape of the function: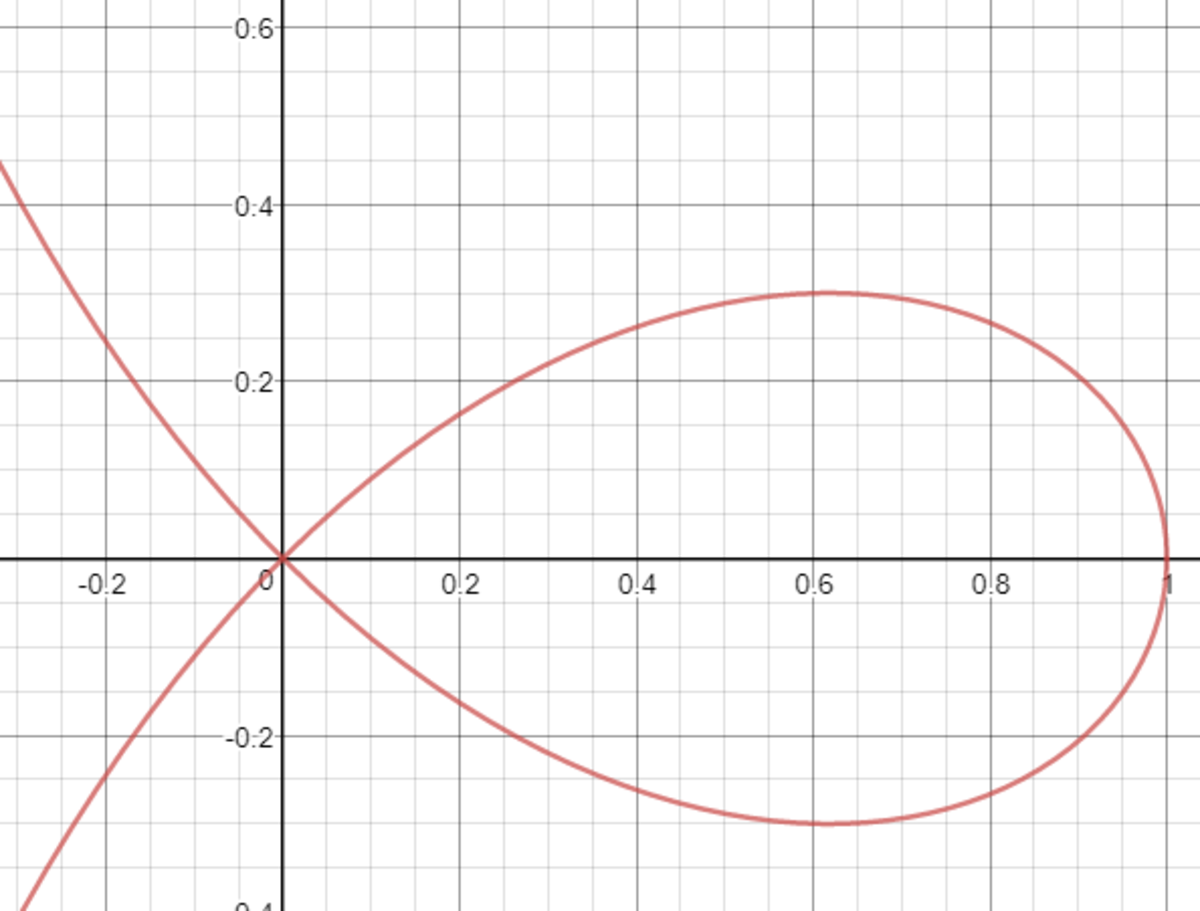

The closed curve is bounded by the values the function takes in two successive values of $\theta$ such that $r = 0$ so let's solve for that: $\cos \theta - \sin \theta \tan \theta = 0 \implies \sin \theta \tan \theta = \cos \theta \implies \tan^2 \theta = 1 \implies \theta = \frac{\pi n}{2} - \frac{\pi}{4}$ . Plugging in $n=0,1$ we get the bounds $-\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4}$ . With this we can describe the area via by following double integral:

$\Large \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \int_{0}^{ \cos \theta - \sin \theta \tan \theta} r dr d \theta = \frac{1}{2} \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} (\cos \theta - \sin \theta \tan \theta)^2 d \theta = \frac{1}{2} \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \cos^2 \theta - 2 \cos \theta \sin \theta \tan \theta + \sin^2 \theta \tan^2 \theta d \theta \\ = \frac{1}{2} \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \cos^2 \theta - 2 \cos \theta \sin \theta \frac{\sin \theta}{\cos \theta} + (1 - cos^2 \theta)\frac{\sin^2 \theta}{\cos^2 \theta} d \theta = \frac{1}{2} \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \cos^2 \theta -2 \sin^2 \theta + \tan^2 \theta - \sin^2 \theta d \theta = \frac{1}{2} \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \cos^2 \theta + \tan^2 \theta - 3 \sin^2 \theta d\theta$

This is now a sum of standard trigonometric integrals and it is equal to $\frac{1}{2} ( 4 - \pi) = 2 - \frac{\pi}{2}$ .

Rewrite the equation to isolate each variable:

$\begin{aligned} x(x - y^2) &= x^3 + y^2 \\ x^2 - xy^2 &= x^3 + y^2 \\ x^2 - x^3 &= y^2 + xy^2 \\ x^2(1 - x) &= y^2(1 + x) \\ y^2 &= \dfrac{x^2(1 - x)}{1 + x}. \end{aligned}$

If we graph this function, we see that it encloses a loop in the interval $x \in [0, 1].$ Since the function is symmetric over the x-axis, we can find the area of the top portion of this loop then multiply by two. The top portion is bounded by the x-axis and the graph of

$y = \sqrt{\dfrac{x^2(1 - x)}{1 + x}} = \dfrac{x(1 - x)}{\sqrt{1 - x^2}},$

so we must find $\displaystyle \int_0^1 \dfrac{x(1 - x)}{\sqrt{1 - x^2}} \, dx.$ Make the substitution $\theta = \arcsin x.$ Then, we have $x = \sin \theta$ and $d \theta = \dfrac{dx}{\sqrt{1 - x^2}}.$ When $x = 0,$ $\theta = 0,$ and when $x = 1,$ $\theta = \dfrac{\pi}{2}.$ All these substitutions yields

$\begin{aligned} \displaystyle \int_0^1 \dfrac{x(1 - x)}{\sqrt{1 - x^2}} \, dx &= \displaystyle \int_0^{\frac{\pi}{2}} (\sin \theta)(1 - \sin \theta) \, d \theta \\ &= \displaystyle \int_0^{\frac{\pi}{2}} (\sin \theta - \sin^2 \theta) \, d \theta \\ &= \displaystyle \int_0^{\frac{\pi}{2}} \left (\sin \theta - \dfrac{1 - \cos 2 \theta}{2} \right ) \, d \theta \\ &= \displaystyle \int_0^{\frac{\pi}{2}} \left (\sin \theta + \dfrac{1}{2} \cos 2 \theta - \dfrac{1}{2} \right ) \, d \theta \\ &= \left [ - \cos \theta + \dfrac{1}{4} \sin 2 \theta - \dfrac{1}{2} \theta \right ]_0^{\frac{\pi}{2}} \\ &= \left ( 0 + 0 - \dfrac{\pi}{4} \right ) - (-1 + 0 - 0) \\ &= 1 - \dfrac{\pi}{4}. \end{aligned}$

The total area is twice this value, which is $2 - \dfrac{\pi}{2} \approx \boxed{0.429}.$