Integration At Its Best
( ∫ 0 1 1 − x 4 x 2 ⋅ d x ) ⋅ ( ∫ 0 1 1 + x 4 d x )
The value of the expression above can be expressed in the form of β γ π . Find β γ .
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
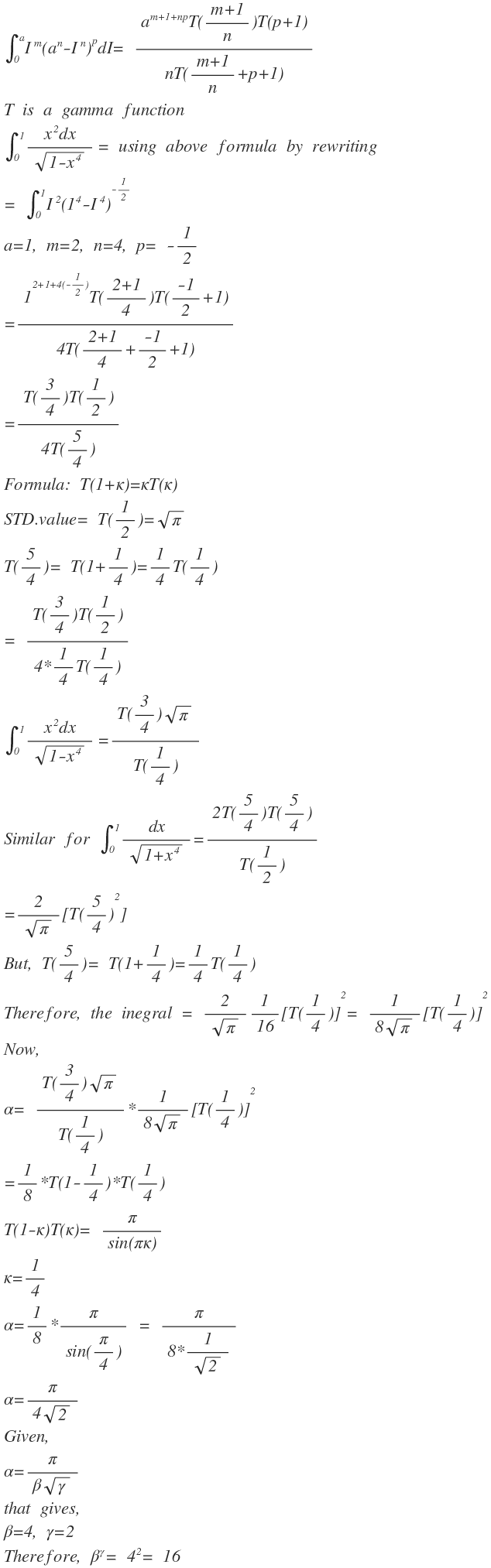
Can u please explain how u got integral 0 to 1 of 1/(1+x^4 )^(1/2) That is how did ur +x become -x.I would be very grateful. i knew first integral from beta fcn but could not do 2nd
Log in to reply
Substitute x = t a n t for the second.Then you will get a function of s i n 2 t ...Then again,substitute s i n 2 t = z and expressing the function in terms of z ,you will get a beta integral.
can you please tell me how did u your beta func. to integrate first integral i dont know how to apply it much.
It becomes easy if u know gamma function