Integration+Trigonometry

Consider where the function $\tan^{-1}\sqrt x$ equals 1: $\tan^{-1}\sqrt x=1\\ x=\tan^2 1\approx2.43$ The function is 0 at x=0, and as x approaches infinity, the function approaches $\frac{\pi}{2}\approx1.57$ . Since $\tan^{-1}\sqrt x$ is a monotonically increasing function, which we can tell from the derivative $\frac{1}{2\sqrt x(1+x)}$ , we know that for $0\leq x<\tan^2 1$ the floor of the function is 0, and for $x\geq\tan^2 1$ the floor of the function is 1: $\left\lfloor\tan^{-1}{\sqrt{x}}\right\rfloor=\begin{cases} 0&0\leq x<\tan^2 1\\ 1&x\geq\tan^2 1\end{cases}$ Now we do the same with the other function.

Consider where the function $\cot^{-1}\sqrt x$ equals 1: $\cot^{-1}\sqrt x=1\\ x=\cot^2 1\approx0.41$ The function is $\frac{\pi}{2}\approx1.57$ at x=0, and as x approaches infinity, the function approaches 0. Since $\cot^{-1}\sqrt x$ is a monotonically decreasing function, which we can tell from the derivative $\frac{-1}{2\sqrt x(1+x)}$ , we know that for $0\leq x<\cot^2 1$ the floor of the function is 1, and for $x\geq\cot^2 1$ the floor of the function is 0: $\left\lfloor\cot^{-1}{\sqrt{x}}\right\rfloor=\begin{cases} 1&0\leq x<\cot^2 1\\ 0&x\geq\cot^2 1\end{cases}$ Here is a graph of these two functions. $\left\lfloor\tan^{-1}{\sqrt{x}}\right\rfloor$ is shown in blue while $\left\lfloor\cot^{-1}{\sqrt{x}}\right\rfloor$ is shown in red.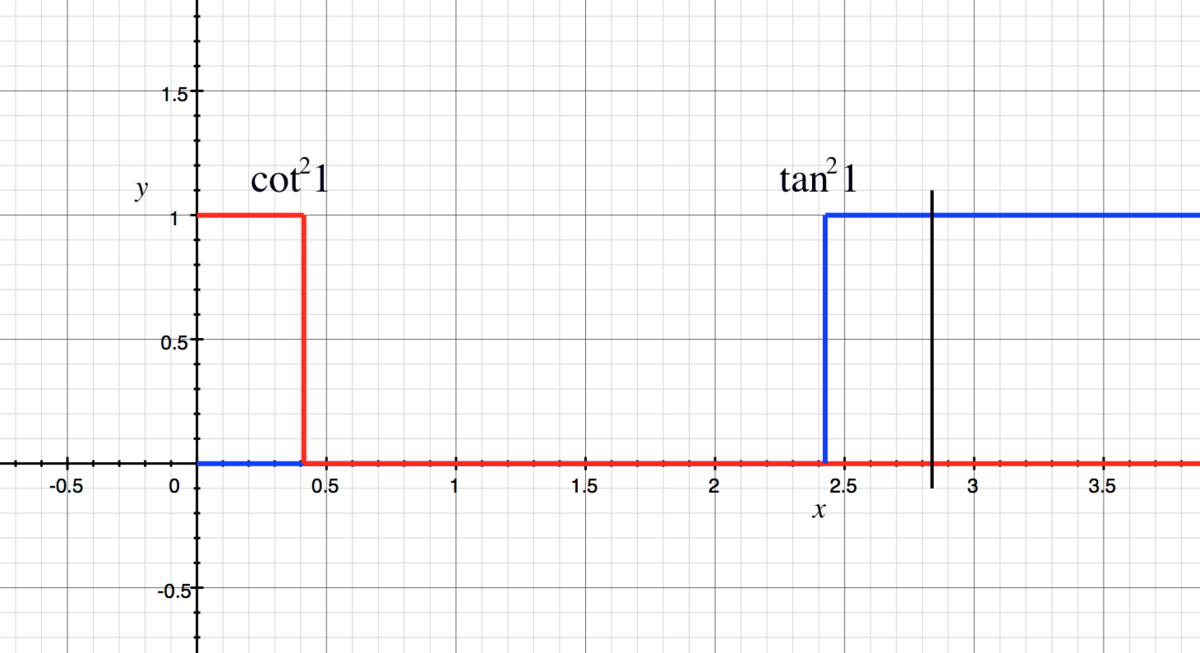 We want to pick a value of a so that the areas under these graphs between 0 and a are equal. Intuitively, this is the black line shown in the graph at $x=\tan^2 1+\cot^2 1$ , so that the two rectangles enclosed by each graph are equal in size.

Now it's just a matter of rearranging the answer using the power reduction formula for cos: $\begin{aligned}a&=\tan^2 1+\cot^2 1\\ &=\sec^2 1+\csc^2 1-2\\\\ &=\frac{\sin^2 1+\cos^2 1}{\sin^2 1\cdot\cos^2 1}-2\\ &=\frac{1-2\sin^2 1\cdot\cos^2 1}{\sin^2 1\cdot\cos^2 1}\\ &=\frac{1-2\cdot\frac{1}{2}(1-\cos2)\cdot\frac{1}{2}(1+\cos2)}{\frac{1}{2}(1-\cos2)\cdot\frac{1}{2}(1+\cos2)}\\ &=\frac{2+2\cos^2 2}{1-\cos^2 2}\\ &=\frac{2+2\cdot\frac{1}{2}(1+\cos4)}{1-\cdot\frac{1}{2}(1+\cos4)}\\ &=\frac{2(3+\cos4)}{1-\cos4}\end{aligned}$ So the answer is $2+3+4+1+4=\boxed{14}$

First consider

$\begin{aligned} I & = \int_0^a \left \lfloor \tan^{-1} \sqrt x\right \rfloor dx & \small \color{#3D99F6} \text{Let }u^2 = x \implies 2u \ du = dx \\ & = \int_0^{\sqrt a} 2\left \lfloor \tan^{-1} u \right \rfloor u\ du \\ & = 2 \int_0^{\tan 1} \left \lfloor \tan^{-1} u \right \rfloor u\ du + 2 \int_{\tan 1}^{\sqrt a} \left \lfloor \tan^{-1} u \right \rfloor u\ du \\ & = 0 + 2 \int_{\tan 1}^{\sqrt a} u\ du & \small \color{#3D99F6} \text{for }\sqrt a < \tan 2 \\ & = a - \tan^2 1 \end{aligned}$

Similarly,

$\begin{aligned} I & = \int_0^a \left \lfloor \cot^{-1} \sqrt x\right \rfloor dx \\ & = \int_0^a \left \lfloor \frac \pi 2 - \tan^{-1} \sqrt x\right \rfloor dx \\ & = 2 \int_0^{\sqrt a} \left \lfloor \frac \pi 2 - \tan^{-1} u \right \rfloor u\ du \\ & = 2 \int_0^{\tan \left(\frac \pi 2-1\right)} u\ du & \small \color{#3D99F6} \text{Note that }\tan \left(\frac \pi 2-1\right) < \tan 1 \\ & = \tan^2 \left(\frac \pi 2-1\right) \\ & = \cot^2 1 \end{aligned}$

Then we have:

$\begin{aligned} a - \tan^2 1 & = \cot^2 1 \\ \implies a & = \frac 1{\tan^2 1} + \tan^2 1 \\ & = \frac {\cos^2 1}{\sin^2 1} + \frac {\sin^2 1}{\cos^2 1} & \small \color{#3D99F6} \text{Note that }\cos^2 \theta = \frac {1+\cos 2\theta}2,\ \sin^2 \theta = \frac {1-\cos 2\theta }2 \\ & = \frac {1+\cos 2}{1-\cos 2} + \frac {1-\cos 2}{1+\cos 2} \\ & = \frac {2\left(1+\cos^2 2\right)}{1-\cos^2 2} \\ & = \frac {2\left(\frac 32+\frac 12 \cos 4\right)}{\frac 12-\frac 12\cos 4} \\ & = \frac {2\left(3+\cos 4\right)}{1-\cos 4} \end{aligned}$

Therefore, $p+q+r+s+t = 2+3+4+1+4 = \boxed{14}$ .