Interacting Families

Geometry Level 3

A family of curves is given by $x^2+kx=ky-y^2$ , where is $k$ is an arbitrary constant. Find a set of orthogonal trajectories to this family.

Details: A set of orthogonal trajectories is comprised of a family of curves whose tangents at any point of intersection with the original curves are at right angles (perpendicular) with the tangents to the original curves. In the choices below $c$ is an arbitrary constant.

The choices are:

A) $\frac{1}{x^2}+\frac{1}{y^2}=\frac{1}{c^2}$
B) $y^2-x^2=c^2$
C) $(y+c)^2-(x-c)^2=1$
D) $y=\frac{c}{x}$
E) $x^2-3y^2=c$
F) $(x-c)^2+(y-c)^2=2c^2$
G) $\frac{y^2}{2}=x^2+c$

The image above obviously represents different families of curves from those described by the equation in this problem.

Inspiration: Hosam Hajjir: Orthogonal Trajectories - Part 2

E C G D F B A

1 solution

Marta Reece
Mar 9, 2017

The original family $x^2+kx=ky-y^2$ can be written as $x^2+kx+y^2-ky=0$ .

This is a set of circles going through the origin. We can see this if we complete the squares.

$x^2+kx+\frac{k^2}{4}+ y^2-ky+\frac{k^2}{4}=2\times\frac{k^2}{4}$

Introducing a new variable $c=\frac{k}{2}$ we can write this as

$x^2+2cx+c^2+ y^2-2cy+c^2=2c^2$

$(x+c)^2+(y-c)^2=2c^2$

The orthogonal trajectories for this family of circles are also a set of circles going through the origin but rotated $90^\circ$ relative to the first. We can see easily that such circles will be perpendicular to the first set at the origin. But any two circles which intersect at right angles at one point must also intersect at right angles at the other due to symmetry.

So the solution looks like this.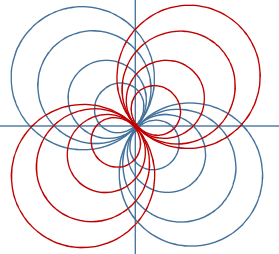 And the formula for it is $(x-c)^2+(y-c)^2=2c^2$ .

Interacting Families

1 solution

0 pending reports