Interesting Case Of Oscillations
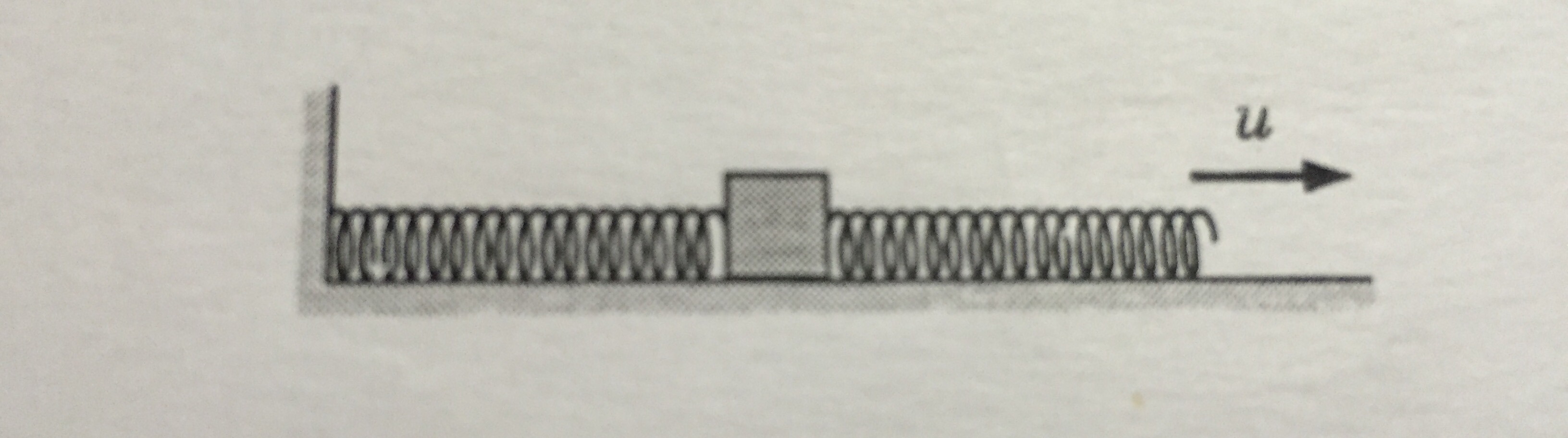
A block of mass placed on a frictionless horizontal floor is connected to two identical springs each of force constant . The left end of the left spring is connected to a fixed support, and the right end of the right spring is free. Initially, the block is at rest, the springs are collinear and relaxed. If someone begins to pull the free end of the right spring with constant velocity away from the wall, find much time passes before the block acquires speed for the first time, and what distance it moves in the time ?
Enter your answer as .
Details and Assumptions
- Take .
The answer is 0.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Hooke's Law
At time t let the position of the mass be x , then the extension of the left spring is x . Because the right end of the right spring is constrained to be at u t , the extension of the right spring is given by u t − x . We therefore have F = k ( u t − 2 x )
a = d t 2 d 2 x .
Because the u t term vanishes under two time derivatives, we can write k ( u t − 2 x ) = 2 − m d t 2 d 2 ( u t − 2 x ) and thus d t 2 d 2 ( u t − 2 x ) = − m 2 k ( u t − 2 x )
Let γ = u t − 2 x . In this form, we can see clearly that this is the governing equation of the simple harmonic oscillator, d t 2 d 2 γ = − m 2 k γ , so that γ = A sin ( ω t + ϕ ) , or 2 x = u t − A sin ( ω t + ϕ ) At t = o , x = 0 , and therefore ϕ = 0 . Taking a time derivative, we have u − 2 v = A ω c o s ( ω t ) , this shows that u − 2 v will be maximum for v = 0 , which gives A = u / ω
For v = u , c o s ( ω t ) = − 1 ⇒ t = π / ω = π 2 k m
Similarly, we can find the distance which comes D = 2 π u 2 k m