Interesting Collision
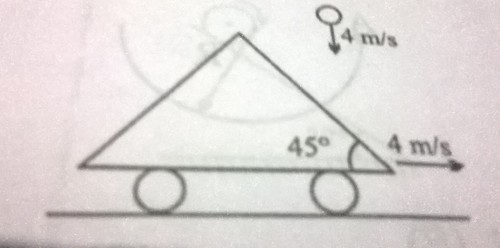 A small ball falling vertically with constant velocity
4
m/s
elastically strikes a massive inclined cart moving with a horizontal velocity of
4
m/s
as shown. What is the rebound velocity of the ball?
A small ball falling vertically with constant velocity
4
m/s
elastically strikes a massive inclined cart moving with a horizontal velocity of
4
m/s
as shown. What is the rebound velocity of the ball?
The answer is 8.94.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
As we know, when small object with momentum p strikes elastically a massive one, like a wall, then it rebounds with the same value of momentum but in opposite direction (velocity vector perpendicular to the wall). So change in momentum is 2 p . Relative velocity of the ball with cart is − V along x-axis, which is directed to the right and − V along y-axis, which is directed upward. So the ball rebounds with the velocity + V along x-axis, and + V along y-axis in cart's frame of reference. Now we go back to our lab frame of reference where ball moves with velocity + 2 V along x-axis (cart's velocity + ball's velocity relative to the cart) and + V along y-axis. Then velocity of rebounded ball is ( 2 V ) 2 + V 2 = V 5 = 4 5 .
so the relative velocity ball with cart is 4sqrt(2). because it strikes elistacally so,it will bounce with 4sqrt(2) too... but remember,we must make it back to relative with earth so,the velocity is 4sqrt(5) equals to,8.9
I would like to clarify Christian's solution.
Let the horizontal be the x-direction, vertical be the y-direction. Since the cart is massive compared to the ball, the cm frame has approximately the same velocity as the cart: v c m = v c a r t = 4 i .
The velocity of the ball in the cm frame is u = v b a l l − v c m = 0 − 4 i + − 4 − 0 j = − 4 i − 4 j .
The velocity in cm frame of elastic collision is reversed: u ′ = − u = 4 i + 4 j .
Transforming back to the lab frame, v ′ b a l l = u ′ + v c m = 8 i + 4 j , which has magnitude 4 5 m/s .
can you explain the solution clearly again.. ?
Velocity of the ball perpendicular to incline = 2 4 m / s
Perpendicular vel of ball w.r.t inclined plane = 2 4 + 2 4 = 4 2 m / s
If after collison perpendicular vel of ball = V then perpendicular velocity w.r.t inclined plane = V − 2 4 , this should be equal to 4 2
so V = 2 1 2 m / s and along inclined plane velocity will be same as 2 4 , so net speed = ( 2 1 2 ) 2 + ( 2 4 ) 2 = 8 0 m / s = 4 5 m / s