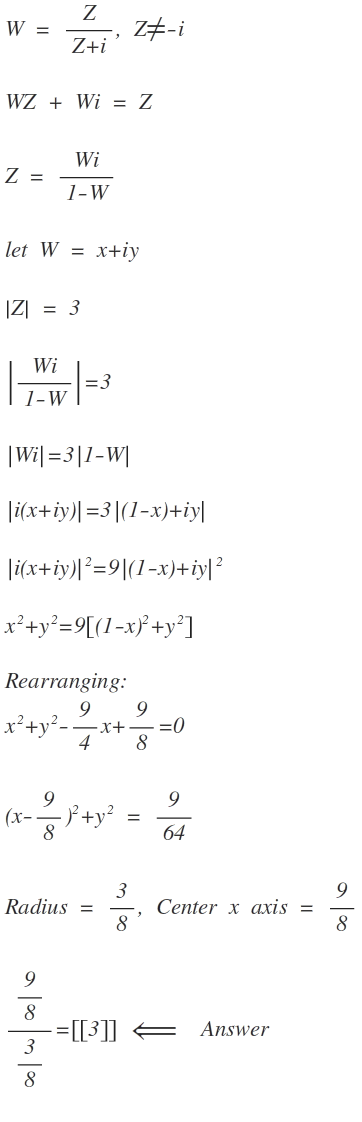Interesting Complex numbers problem
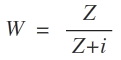 A transformation T from the Z plane to the W plane is given by
A transformation T from the Z plane to the W plane is given by
W = Z + i Z , Z = − i
The circle with equation ∣ Z ∣ = 3 is mapped by T onto the Curve "C" which is also a circle.
Find the value of G/R where G is the x value of the coordinate of the center of the circle C and R is the radius of the circle C
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The transformation T is an example of a fractional linear transformation z ↦ c z + d a z + b . It is a general fact that such transformations send "clircles" to "clircles" (where a "clircle" is a circle or a line).
Three points in the plane determine a unique clircle. The points 3 , ± 3 i on ∣ Z ∣ = 3 map to 1 0 9 − 3 i , 4 3 , 2 3 . It's not hard to see that these points lie on the circle with radius 3 / 8 centered at z = 9 / 8 . So the answer is 3 .
(In fact, the computations are easier if you note that ± 3 , ± 3 i map to 1 0 9 ∓ 3 i , 4 3 , 2 3 , and drawing those four points makes it clear that the center of the circle must lie on the x -axis by symmetry considerations, and so it must be halfway between 4 3 and 2 3 . )
(Another way to see that the center of C must be on the x -axis is to use the general fact that T is conformal, i.e. preserves angles. The imaginary axis is perpendicular to the original circle, so the image of the imaginary axis must be perpendicular to the new circle. But the image of the imaginary axis is the real axis, and the only way for the real axis to be perpendicular to the circle is if it goes through the center.)