Interesting geometry problem (3 circle puzzle)
 Interesting geometry problem (3 circle puzzle)Mind Your Concept
Interesting geometry problem (3 circle puzzle)Mind Your Concept
In the given figure centres of the three circles are marked. With the measurement given. Find the radius of blue circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
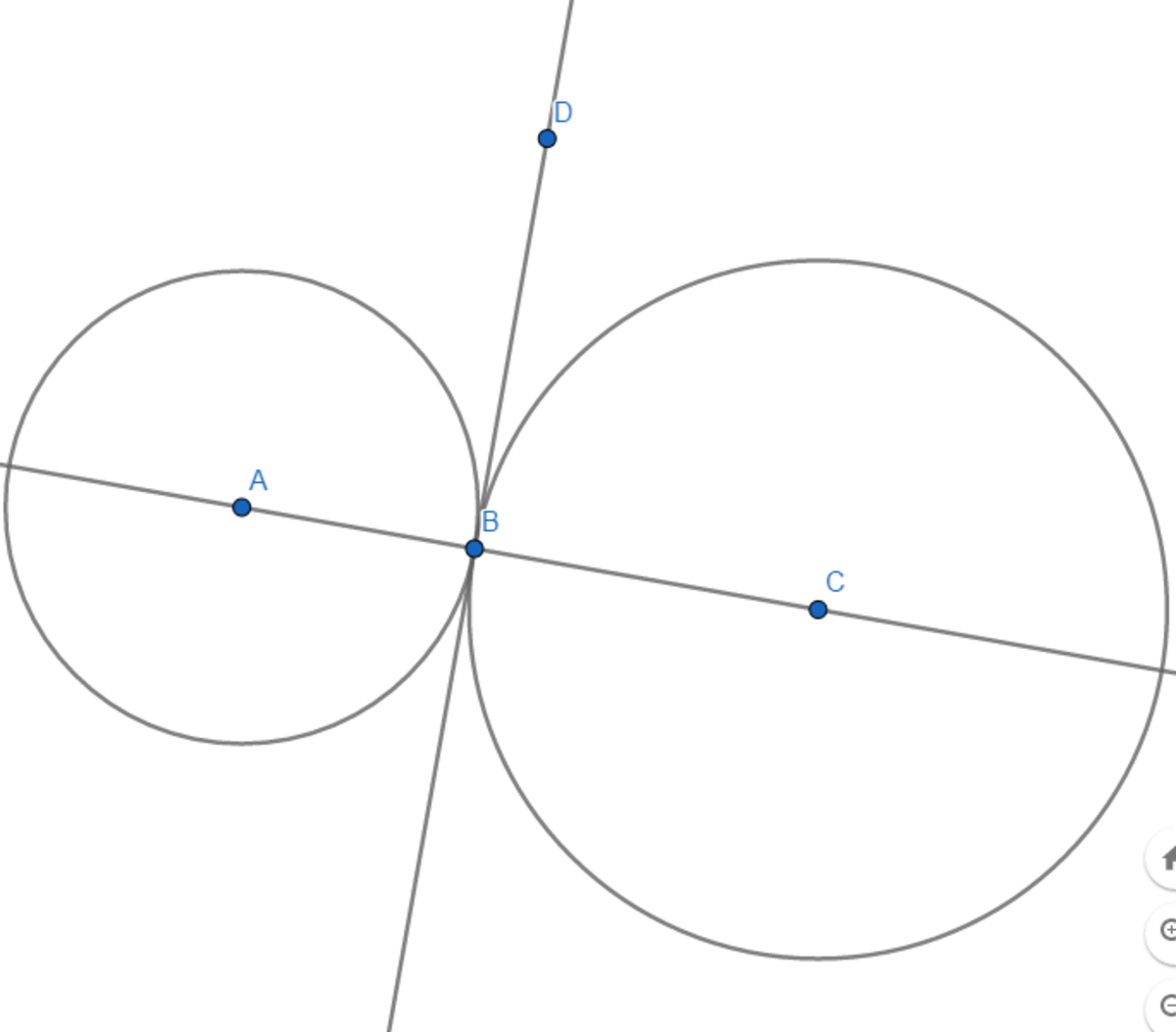 firstly if there are two circles with centres
A
,
C
and intersects at only point
B
then
B
∈
[
A
C
]
firstly if there are two circles with centres
A
,
C
and intersects at only point
B
then
B
∈
[
A
C
]
because these two circles tangent on point B will be the same line
∠ A B D = 9 0 ∘ , ∠ C B D = 9 0 ∘ and sum of them is 1 8 0 ∘ which shows that A , B , C are linear
let big circles radius is R and little ones r
2 R + 6 = 2 r + 1 2 ⇒ R = r + 3
draw the line segment between black circles centres the little triangle will be 4 5 ∘ − 4 5 ∘ − 9 0 ∘ triangle
on the big right triangle : ( r + 3 + r ) 2 + ( r + 3 + 6 ) 2 = ( 1 2 + r ) 2
⇒ 2 r 2 + 3 r − 2 7 = 0
( 2 r + 9 ) ( r − 3 ) = 0 Hence r = 3 . blue circles radius is 1 2 + 2 r = 1 8
The key observation is that the triangle formed by the three centres of the circles has a right-angle at the centre of the larger black circle (note the marked 4 5 ∘ angle).
Let the radius of the blue circle be r , the larger black circle a and the smaller black circle b . Then we get the following equations:
r r ( a + 6 ) 2 + ( a + b ) 2 = 2 a + 6 = 2 b + 1 2 = ( b + 1 2 ) 2
Substituting for a and b in the third equation, we get the quadratic r 2 − 2 1 r + 5 4 = 0 ; solving and discarding the smaller root (which makes a and b negative), we get r = 1 8 .