Interesting geometry problems- By Mind Your Concept.
Geometry
Level
3
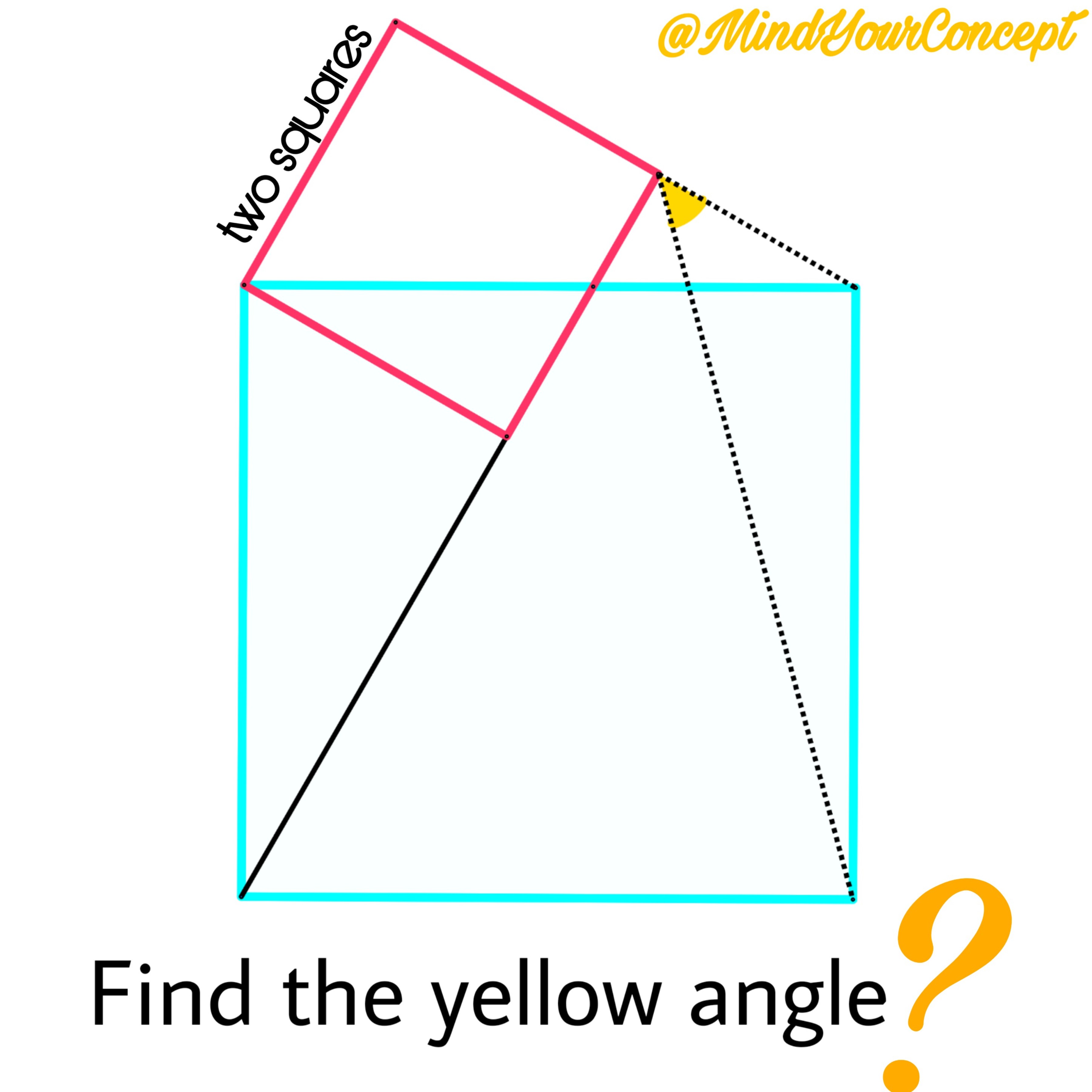 In a blue square a red square is drawn as shown. Find the yellow angle?
In a blue square a red square is drawn as shown. Find the yellow angle?
It is not a constant
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the large blue square be A B C D with side length 1 , the small red square be A E F G , ∠ A D G = α and the yellow angle B F C = θ . We note that △ A B E and △ A D G are congruent. Then B F = B E − E F = cos α − sin α . By sine rule , we have:
B C sin ∠ B F C 1 sin θ sin θ ( cos α − sin α ) sin θ cos α − sin θ sin α sin θ cos α tan θ ⟹ θ = B F sin ∠ B C E = cos α − sin α sin ( 1 8 0 ∘ − ( 9 0 ∘ + α ) − θ ) = sin ( 9 0 ∘ − α − θ ) = cos ( θ + α ) = cos θ cos α − sin θ sin α = cos θ cos α = 1 = 4 5 ∘