Interesting Incircle
A B C is a triangle with ∠ B A C = 6 0 ∘ . It has an incircle Γ , which is tangential to B C at D . It is given that B D = 3 and D C = 4 . What is the value of [ A B C ] 2 ?
Details and assumptions
[ P Q R S ] denotes the area of figure P Q R S .
The answer is 432.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Let the incircle tangential to A C at E and tangential to A B at F
Note that B F O D , D O E C and A F O E are all kites so we have that
B D = B F , A F = A E , C E = C D
and let A F be x so the length of the triangles are A B = x + 3 , B C = 7 , C A = x + 4
By Cosine Rule, A B 2 + A C 2 − 2 × A B × A C × c o s ∠ B A C = B C 2
( x + 3 ) 2 + ( x + 4 ) 2 − 2 × ( x + 3 ) × ( x + 4 ) × c o s 6 0 ∘ = 7 2
x 2 + 6 x + 9 + x 2 + 8 x + 1 6 − 2 × ( x 2 + 7 x + 1 2 ) × 2 1 = 4 9
x 2 + 7 x + 1 3 = 4 9 → x 2 + 7 x − 3 6 = 0
x 1 , 2 = 2 ( 1 ) − 7 ± 7 2 − 4 ( 1 ) ( − 3 6 ) → x 1 , 2 = 2 − 7 ± 1 9 3 ,
x = 2 − 7 − 1 9 3 is disqualified because x must be more than 0.
so x = 2 − 7 + 1 9 3
[ A B C ] = 2 1 × A B × A C × s i n ( ∠ B A C )
[ A B C ] = 2 1 × ( 2 − 7 + 1 9 3 + 3 ) × ( 2 − 7 + 1 9 3 + 4 ) × 2 3
[ A B C ] = 4 3 2
Hence [ A B C ] 2 = 4 3 2
Sejam E,F as projeções ortogonais do centro I do incírculo nos segmentos AB e AC, respectivamente.
Os triângulos EIB e DIB são congruentes. Os triângulos DIC e FIC são congruentes. Os triângulos AIE e AIF são congruentes.
Portanto, EB=BD=3, FC=DC=4 e AE=AF = x
Aplicando a Lei dos Cossenos no triângulo ABC, temos:
7² = (3+x)² + (4+x)² - 2.(0.5)(3+x)(4+x) x²+7x-36=0 e como x é positivo, então:
x = (-7 + \sqrt(139) )/2
Pela Lei das Áreas, a área do triângulo ABC é :
[ABC] = (3+x)(4+x)sin(60º)/2
Substituindo o valor de x encontrado:
[ABC] = 12.sqrt(3)
Portanto, [ABC]² = 12² . 3 = 432
Step1 : Let E,F be the point of tangency on CA and AB respectively. Let, AF=AE = 'x' We have AB = x+3 and AC= x+4 in that case and BC= 7
Step 2: Apply Cosine Rule and you get (x+3)^2 + (x+4)^2 - 49 = 2 * cos60 * (x +3)*(x+4)
Simplifying u get : x^2 + 7x -36 = 0 ---eq 1
Solving we get x= 3.44
Step 3: Appy Sine formula for Area
[ABC] = 1/2 * AB AC *sin60 = 1/2 *(x+3) (x+4)* sqrt3 /2
[ABC] = sqrt 3 /4 * (x^2 + 7x+12) = sqrt 3 /4 * 48 (from eq1) = sqrt 3 *12
Hence, [ABC]^2 = 144 *3 = 432
Let the centre of the Γ be O .
Let the radius of the Γ be r
Let the Γ be tangential to A B and A C at E and F respectively
Let s be half of the perimeter of Δ A B C
O B = O B
O E = r = O D
∠ O E B = 9 0 ∘ = ∠ O D B
∴ Δ O E B ≅ Δ O D B
E B = B D = 3
O C = O C
O D = r = O F
∠ O D C = 9 0 ∘ = ∠ O F C
∴ Δ O D C ≅ Δ O E C
E C = D C = 4
O A = O A
O E = r = O F
∠ O E A = 9 0 ∘ = ∠ O F A
∴ Δ O E A ≅ Δ O F A
∠ O A E = ∠ O A F = 2 1 ( ∠ E A F ) = 3 0 ∘
∴ O A = 2 ⋅ O E = 2 r
A F = A E = O A 2 − O E 2 = 4 r 2 − r 2 = 3 r 2 = 3 ⋅ r
s = 2 A B + B C + A C = 2 A B + E B + B D + D C + E C + A E = 2 3 ⋅ r + 3 + 3 + 4 + 4 + 3 ⋅ r = 7 + 3 ⋅ r
By Heron's Formula , we have
( s ) ( 7 + 3 ⋅ r − ( 3 + 3 ⋅ r ) ) ( 7 + 3 ⋅ r − 7 ) ( 7 + 3 ⋅ r − ( 4 + 3 ⋅ r ) )
= A r e a o f Δ A B C = s ⋅ r
( s ) ( 4 ) ( 3 ⋅ r ) ( 3 ) = ( s ⋅ r ) 2
1 2 ⋅ s ⋅ ( 3 ⋅ r ) = s 2 ⋅ r 2
1 2 3 = s r
( A r e a o f Δ A B C ) 2 = s r 2 = ( 1 2 3 ) 2 = 432
consider triangle ABC in clockwise order(Order of vertex does not matter). Let Incircle touches sides AC and AB at E and F respectively. Then clearly BD=BF=3,CD=CE=4,AE=AF=x(say).(Because length of tangents from a point on circle is equal.) Now From Cosine Rule Cosine(BAC)=(AB^2+AC^2-BC^2)/2(AB AC). Putting lengths of sides in this equation gives x^2+7x=36. Area of Triange ABC=(1/2) AB AC Sin(60)=1/2 (x+3) (x+4) sin60= 1/2 (x^2+7x+12) (sqrt(3)/2) .Putting value of x^2+7x=36. We get [ABC]=12 sqrt(3). So [ABC]^2=432
Let point of contact of incircle Γ with AB and AC be E and F .
As , BD = 3 => BE = 3 (because tangents are drawn from B to incircle Γ , So length of tangents are equal ) , same for CD = 4 => CF = 4 .
Let , AF = AE = k .
So , AB = k+3 , AC = k+4 & BC = 7 .
Using Law of cosine for ∠BAC ,
$ cos(BAC) = (1/2) = [ (AB)^2 + (AC)^2 - (BC)^2] / (2
AC
AB) $ ∴ $ (k+3)^2 + (k+4)^2 - 7^2 = (k+3)(k+4) $
$ k^2 + 7k - 36 = 0 . $
Two solutions are there , we are interested in positive one ,
$ k = \frac{1}{2} (-7 + \sqrt(193)) $
$ AB = \frac{1}{2} (-1 + \sqrt(193)) , AC = \frac{1}{2} (1 + \sqrt(193)) $
We now have three sides of triangle . We can use Heron's Formula for Area of Triangle , $ AB = c , BC = a , AC = b $ there are many ways of writing heron's formula one of them is as below : [ABC] = $ \frac{1}{4} \sqrt( (a^{2} + b^{2} + c^{2} )^{2} - 2(a^{4} + b^{4} + c^{4} ) ) .
$ b^{2} + c^{2} = (b+c)^{2} - 2bc = 97 $
$ b^{4} + c^{4} = (b^{2} + c^{2})^{2} - 2 (bc)^{2} = 4801 $
Thus , $ [ABC]^2 = \frac{1}{16} ( 6912) = 432 . $
Let I be the center of the circle and r be the radius. We have angle ABC + angle ACB = 120, so angle IBC + angle ICD = 60 Also tanIBC = r/3 tanICD = r/4 tan(60-IBC)=r/4 (tan60 - tanIBC) / (1+tan60tanIBC) = r/4 (tan60 - r/3) / (1 + tan60r/3) = r/4
Solving for r we get r = (-7sqrt(3) + sqrt(579)) / 6
Let E and F be the points where the circle touches AB and AC respectively
Then AE = AF = r / tan30 AB = r/tan30 + 3 AC = r/tan30 +4
Thus area of ABC = 0.5 AB ACsin60 = 432
Let the incircle touch AB at M and AC at N. Let AM = x. Since, tangents from same point are equal. AN = AM = x BM = BD=3 CN=CD=4 s(semiperimeter) = (14+2x)/2 =7+x Area = 1/2 bc sinA = \sqrt{3}/4*(3+x)(4+x) radius of incircle = area/s Let the center of incircle be O. In right triangle AOM. x = r cot(60/2) = r \sqrt{3} but r = area/s Hence, x = 3/4 * (3+x)(4+x)/(7+x) Crossmultiplying and simplifying x^2 +7x -36 =0 or x^2 +7x =36 (i)
Now, area = \sqrt{3}/4 (x^2+7x+12) = \sqrt{3}/4 (0+48) = 12 \sqrt{3} (area)^2 = 144*3 = 432. QED
Let ABC be a triangle with ∠ BAC = 60 degrees.
Let Γ be incircle of triangle ABC.
Let D , E , F be points of intersection of incircle with sides BC , CA and
AB respectively.
AE = AF , BD = BF , CD = CE.
Let AE = AF = x.
Therefore , AB = x + 3 , AC = x +4 , BD = 3 , DC = 4.
From cosine rule ,
Cos A = ( Sqr(AB) + Sqr(AC) - Sqr(BC) ) / 2 * AB * AC
( Sqr (x) = x * x )
=> Cos 60 = ( Sqr(x+3) + Sqr(x+4) - Sqr (7) )/ 2 * (x+3) * (x+4)
=> 0.5 * 2 * ( Sqr(x) +7x +12 ) = 2 * Sqr (x) + 14x +25 - 49
=> Sqr(x) +7x +12 = 2*Sqr(x) +14x +- 24
=> Sqr(x) + 7x - 36 = 0
Therefore , x = ( - 7 + Root( Sqr(7) - 4 * 1 * (-36)) ) / 2*1
( Eg.Root(49) = 7 )
x = ( -7 + Root(193) ) / 2
Therefore , AB = x + 3 = ( Root(193) - 1 ) / 2
AC = x + 4 = ( Root(193) + 1 ) / 2
So , Area of triangle ABC = (1/2) * AB * AC * Sin60
= (0.5) * (( Root(193) - 1 ) / 2) * (( Root(193) + 1 ) / 2) * Sin60
= (0.5) * (( Sqr(Root(193)) -1) / 4) * Sin60
=((193-1)/8) * Sin60
=(192/8) * Sin60
=(24) * Sin60
Therefore ,
Sqr(Area of Triangle ABC) = Sqr( 24* Sin60 )
= 576 * Sqr(Root(3)/2)
= 576 * 3 / 4
= 144 * 3
= 432 .
7r/(12-r^2)=sqrt(3), S=r(sqrt(3)r+7)=12sqrt(3)
The first important thing to note is that the intersections of an incircle split sides A B , B C , and A C into lengths of x and y , y and z , and x and z , respectively. Let E be the intersection of the incircle and side A B , and let F be the intersection of the incircle on side A C . Thus, E B = E D = 3 , D C = F C = 4 , and A E = A F .
Next, using the information that the incircle is formed by the angle bisectors and that ∠ B A C = 6 0 ∘ , we get that A E = A F = r 3 .
With this information, we can set up two equations to find the area and equate them together, namely that A = s r = s ( s − a ) ( s − b ) ( s − c ) , where s is the semiperimeter. Substituting in the appropriate values for s , a , b , and c and solving for r , we come to r = 2 3 1 9 3 − 7 . Substituting this value of r back into either of the equations to find Area and squaring we come to the surprisingly clean number of 432 , our final answer.
Solution 1: Let the distance from A to the circle be y . Applying cosine rule to ∠ B A C , we get that cos 6 0 ∘ = 2 ( y + 3 ) ( y + 4 ) ( y + 3 ) 2 + ( y + 4 ) 2 − 7 2 , or that y = 2 − 7 + 1 9 3 (ignore negative root).
This allows us to calculate the area using the sine rule formula, giving
[ A B C ] = 2 1 ( y + 3 ) ( y + 4 ) sin 6 0 ∘ = 2 1 ⋅ 2 1 9 3 − 1 ⋅ 2 1 9 3 + 1 ⋅ 2 3 = 1 6 1 9 2 3 .
Thus, [ A B C ] 2 = 4 3 2 .
Solution 2: We will use various formulas for the geometric measurements.
Let the corresponding lengths of the triangle are
a
,
b
,
c
, and the corresponding angles be
α
,
β
,
γ
.
The semi perimeter is
2
a
+
b
+
c
.
Heron's formula states that
[
A
B
C
]
=
s
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
.
The radius of the incircle is
r
=
s
[
A
B
C
]
=
s
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
.
Let
E
be the tangent between
Γ
and
A
C
.
We have
B
D
=
s
−
c
,
C
D
=
s
−
b
and
A
E
=
s
−
a
.
Then
tan
2
α
=
A
E
r
=
s
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
.
Hence, we can calculate that [ A B C ] = tan 2 α ( s − b ) ( s − c ) = 3 × 4 × 3 . Hence [ A B C ] 2 = 4 3 2 .
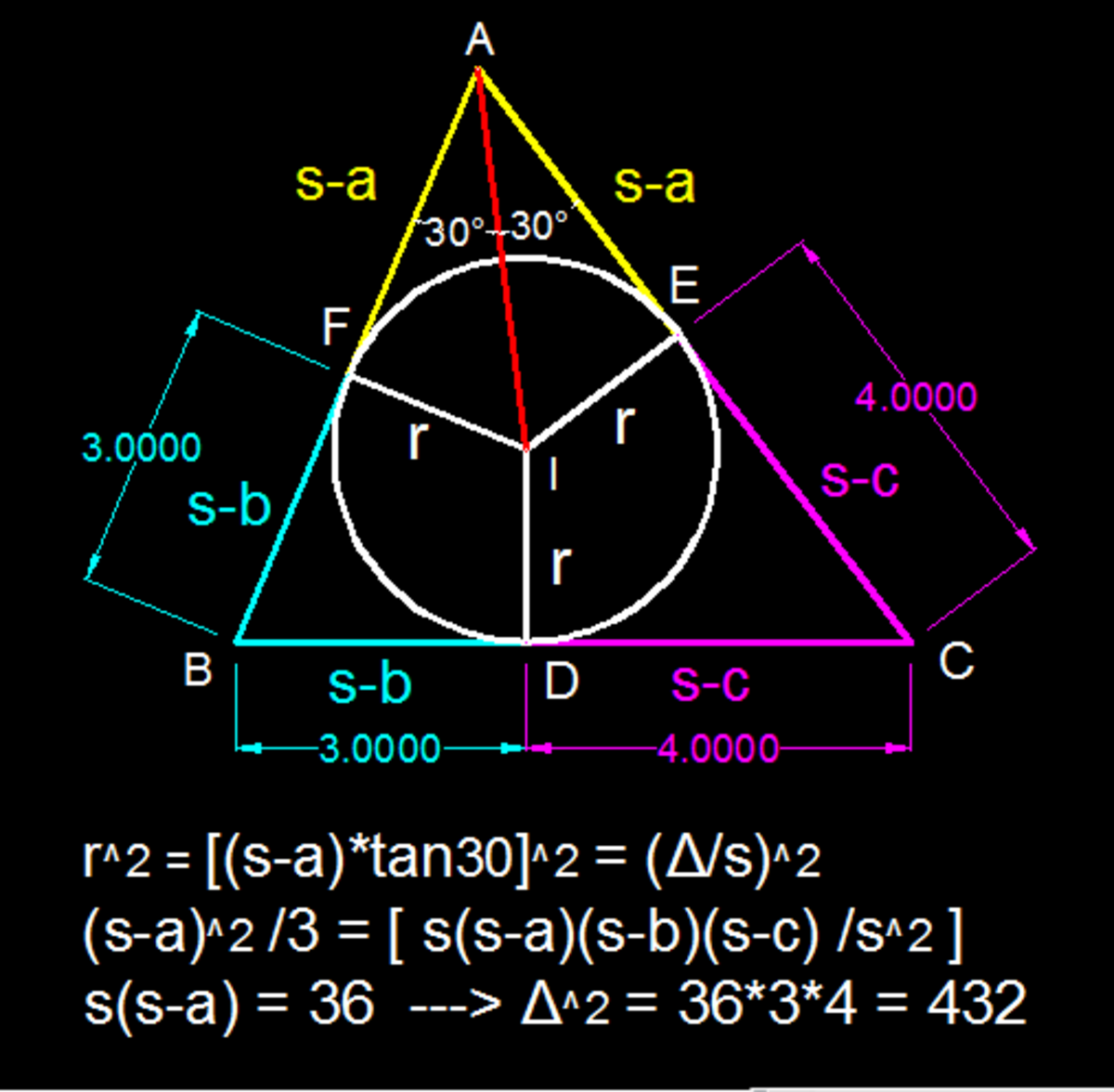
B C = B D + D C = 7 . Let E and F denote the points of tangency of the incircle on segments A C and A B , respectively. Let A E = A F = x . By the Law of Cosines, we have
B C 2 = A B 2 + A C 2 − 2 ( A B ) ( A C ) ( cos A ) ⇒ 7 2 = ( x + 3 ) 2 + ( x + 4 ) 2 − 2 ( x + 3 ) ( x + 4 ) ( cos 6 0 )
Simplifying yields x 2 + 7 x = 3 6 .
[ A B C ] = 2 ( A B ) ( A C ) ( sin A ) = 2 ( x + 3 ) ( x + 4 ) ( sin 6 0 ) = 4 ( x 2 + 7 x + 1 2 ) 3 = 4 ( 3 6 + 1 2 ) 3 = 1 2 3
Thus, [ A B C ] 2 = 4 3 2 .