Interesting Incircle

$BC = BD + DC = 7$ . Let $E$ and $F$ denote the points of tangency of the incircle on segments $AC$ and $AB$ , respectively. Let $AE = AF = x$ . By the Law of Cosines, we have

$BC^2 = AB^2 + AC^2 - 2(AB)(AC)(\cos A) \Rightarrow$ $7^2 = (x+3)^2 + (x+4)^2 - 2(x+3)(x+4)(\cos 60)$

Simplifying yields $x^2 + 7x = 36$ .

$[ABC] = \frac{(AB)(AC)(\sin A)}{2} = \frac{(x+3)(x+4)(\sin 60)}{2} =$ $\frac{(x^2 + 7x + 12)\sqrt{3}}{4} = \frac{(36 + 12)\sqrt{3}}{4} = 12\sqrt{3}$

Thus, $[ABC]^2 = \boxed{432}$ .

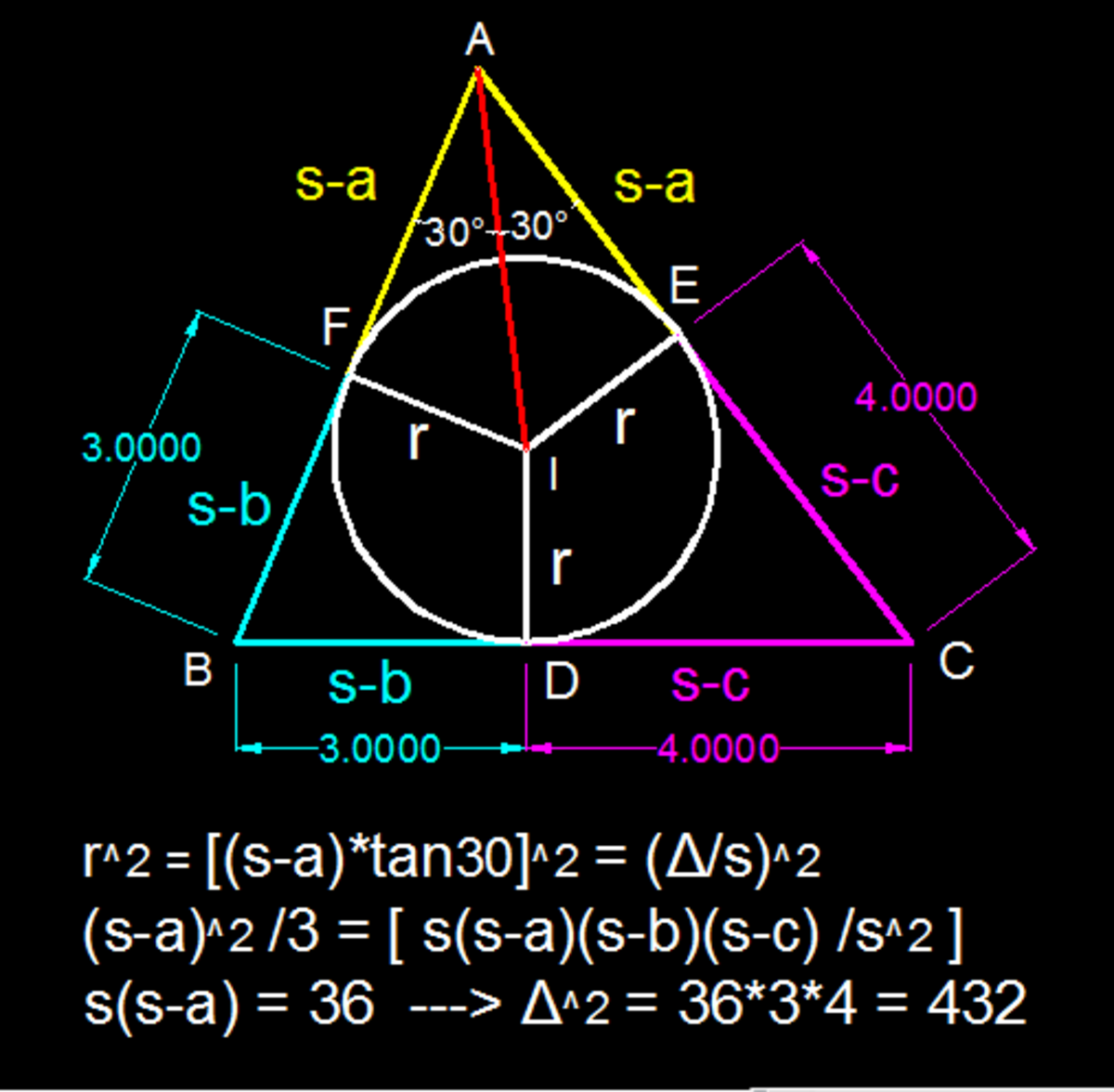
Let the incircle tangential to $AC$ at $E$ and tangential to $AB$ at $F$

Note that $BFOD$ , $DOEC$ and $AFOE$ are all kites so we have that

$BD= BF, AF = AE, CE = CD$

and let $AF$ be $x$ so the length of the triangles are $AB= x+3 , BC = 7 , CA = x+4$

By Cosine Rule, $AB^2 + AC^2 - 2 \times AB \times AC\times cos \angle BAC = BC^2$

$(x+3)^2 + (x+4)^2 - 2 \times(x+3)\times(x+4) \times cos 60^\circ = 7^2$

$x^2 + 6x +9 + x^2 + 8x + 16 - 2 \times(x^2 + 7x + 12) \times \frac{1}{2}=49$

$x^2+7x+13 = 49 \rightarrow x^2 + 7x -36 =0$

$x_{1,2} = \frac{-7 \pm \sqrt{7^2-4(1)(-36)}}{2(1)} \rightarrow$ $x_{1,2} = \frac{-7 \pm \sqrt{193}}{2}$ ,

$x= \frac{-7 - \sqrt{193}}{2}$ is disqualified because $x$ must be more than 0.

so $x= \frac{-7 + \sqrt{193}}{2}$

$[ABC] = \frac{1}{2} \times AB \times AC \times sin(\angle BAC)$

$[ABC] = \frac{1}{2} \times (\frac{-7 + \sqrt{193}}{2}+3)\times(\frac{-7 + \sqrt{193}}{2}+4)\times\frac{\sqrt{3}}{2}$

$[ABC] = \sqrt{432}$

Hence $[ABC]^2 = 432$

Sejam E,F as projeções ortogonais do centro I do incírculo nos segmentos AB e AC, respectivamente.

Os triângulos EIB e DIB são congruentes. Os triângulos DIC e FIC são congruentes. Os triângulos AIE e AIF são congruentes.

Portanto, EB=BD=3, FC=DC=4 e AE=AF = x

Aplicando a Lei dos Cossenos no triângulo ABC, temos:

7² = (3+x)² + (4+x)² - 2.(0.5)(3+x)(4+x) x²+7x-36=0 e como x é positivo, então:

x = (-7 + \sqrt(139) )/2

Pela Lei das Áreas, a área do triângulo ABC é :

[ABC] = (3+x)(4+x)sin(60º)/2

Substituindo o valor de x encontrado:

[ABC] = 12.sqrt(3)

Portanto, [ABC]² = 12² . 3 = 432

Step1 : Let E,F be the point of tangency on CA and AB respectively. Let, AF=AE = 'x' We have AB = x+3 and AC= x+4 in that case and BC= 7

Step 2: Apply Cosine Rule and you get (x+3)^2 + (x+4)^2 - 49 = 2 * cos60 * (x +3)*(x+4)

Simplifying u get : x^2 + 7x -36 = 0 ---eq 1

Solving we get x= 3.44

Step 3: Appy Sine formula for Area

[ABC] = 1/2 * AB AC *sin60 = 1/2 *(x+3) (x+4)* sqrt3 /2

[ABC] = sqrt 3 /4 * (x^2 + 7x+12) = sqrt 3 /4 * 48 (from eq1) = sqrt 3 *12

Hence, [ABC]^2 = 144 *3 = 432

Let the centre of the $\Gamma$ be $O$ .

Let the radius of the $\Gamma$ be $r$

Let the $\Gamma$ be tangential to $AB$ and $AC$ at $E$ and $F$ respectively

Let $s$ be half of the perimeter of $\Delta ABC$

$OB$ = $OB$

$OE$ = $r$ = $OD$

$\angle OEB$ = $90^\circ$ = $\angle ODB$

$\therefore \Delta OEB \cong \Delta ODB$

$EB$ = $BD$ = $3$

$OC$ = $OC$

$OD$ = $r$ = $OF$

$\angle ODC$ = $90^\circ$ = $\angle OFC$

$\therefore \Delta ODC \cong \Delta OEC$

$EC$ = $DC$ = $4$

$OA$ = $OA$

$OE$ = $r$ = $OF$

$\angle OEA$ = $90^\circ$ = $\angle OFA$

$\therefore \Delta OEA \cong \Delta OFA$

$\angle OAE$ = $\angle OAF$ = $\frac{1}{2}(\angle EAF)$ = $30^\circ$

$\therefore$ $OA$ = $2\cdot OE$ = $2r$

$AF$ = $AE$ = $\sqrt{OA^2 - OE^2}$ = $\sqrt{4r^2 - r^2}$ = $\sqrt{3r^2}$ = $\sqrt{3} \cdot r$

$s$ = $\frac{AB + BC + AC}{2}$ = $\frac{AB+EB+BD+DC+EC+AE}{2}$ = $\frac{\sqrt{3} \cdot r + 3 + 3 + 4 + 4 + \sqrt{3} \cdot r}{2}$ = $7 + \sqrt{3} \cdot r$

By Heron's Formula , we have

$\sqrt{(s)( 7 + \sqrt{3} \cdot r - (3 + \sqrt{3} \cdot r))( 7 + \sqrt{3} \cdot r - 7)( 7 + \sqrt{3} \cdot r - (4 + \sqrt{3} \cdot r))}$

= $Area of \Delta ABC$ = $s \cdot r$

$(s)(4)(\sqrt{3} \cdot r)(3)$ = $(s \cdot r)^2$

$12 \cdot s \cdot (\sqrt{3} \cdot r)$ = $s^2 \cdot r^2$

$12 \sqrt{3}$ = $sr$

$(Area of \Delta ABC)^2$ = $sr^2$ = $(12 \sqrt{3})^2$ = 432

consider triangle ABC in clockwise order(Order of vertex does not matter). Let Incircle touches sides AC and AB at E and F respectively. Then clearly BD=BF=3,CD=CE=4,AE=AF=x(say).(Because length of tangents from a point on circle is equal.) Now From Cosine Rule Cosine(BAC)=(AB^2+AC^2-BC^2)/2(AB AC). Putting lengths of sides in this equation gives x^2+7x=36. Area of Triange ABC=(1/2) AB AC Sin(60)=1/2 (x+3) (x+4) sin60= 1/2 (x^2+7x+12) (sqrt(3)/2) .Putting value of x^2+7x=36. We get [ABC]=12 sqrt(3). So [ABC]^2=432

Let point of contact of incircle Γ with AB and AC be E and F . As , BD = 3 => BE = 3 (because tangents are drawn from B to incircle Γ , So length of tangents are equal ) , same for CD = 4 => CF = 4 . Let , AF = AE = k . So , AB = k+3 , AC = k+4 & BC = 7 . Using Law of cosine for ∠BAC , $ cos(BAC) = (1/2) = [ (AB)^2 + (AC)^2 - (BC)^2] / (2 AC AB) $ ∴ $ (k+3)^2 + (k+4)^2 - 7^2 = (k+3)(k+4) $
$ k^2 + 7k - 36 = 0 . $ Two solutions are there , we are interested in positive one , $ k = \frac{1}{2} (-7 + \sqrt(193)) $
$ AB = \frac{1}{2} (-1 + \sqrt(193)) , AC = \frac{1}{2} (1 + \sqrt(193)) $

We now have three sides of triangle . We can use Heron's Formula for Area of Triangle , $ AB = c , BC = a , AC = b $ there are many ways of writing heron's formula one of them is as below : [ABC] = $ \frac{1}{4} \sqrt( (a^{2} + b^{2} + c^{2} )^{2} - 2(a^{4} + b^{4} + c^{4} ) ) .

$ b^{2} + c^{2} = (b+c)^{2} - 2bc = 97 $ $ b^{4} + c^{4} = (b^{2} + c^{2})^{2} - 2 (bc)^{2} = 4801 $
Thus , $ [ABC]^2 = \frac{1}{16} ( 6912) = 432 . $

Let I be the center of the circle and r be the radius. We have angle ABC + angle ACB = 120, so angle IBC + angle ICD = 60 Also tanIBC = r/3 tanICD = r/4 tan(60-IBC)=r/4 (tan60 - tanIBC) / (1+tan60tanIBC) = r/4 (tan60 - r/3) / (1 + tan60r/3) = r/4

Solving for r we get r = (-7sqrt(3) + sqrt(579)) / 6

Let E and F be the points where the circle touches AB and AC respectively

Then AE = AF = r / tan30 AB = r/tan30 + 3 AC = r/tan30 +4

Thus area of ABC = 0.5 AB ACsin60 = 432

Let the incircle touch AB at M and AC at N. Let AM = x. Since, tangents from same point are equal. AN = AM = x BM = BD=3 CN=CD=4 s(semiperimeter) = (14+2x)/2 =7+x Area = 1/2 bc sinA = \sqrt{3}/4*(3+x)(4+x) radius of incircle = area/s Let the center of incircle be O. In right triangle AOM. x = r cot(60/2) = r \sqrt{3} but r = area/s Hence, x = 3/4 * (3+x)(4+x)/(7+x) Crossmultiplying and simplifying x^2 +7x -36 =0 or x^2 +7x =36 (i)

Now, area = \sqrt{3}/4 (x^2+7x+12) = \sqrt{3}/4 (0+48) = 12 \sqrt{3} (area)^2 = 144*3 = 432. QED

Let ABC be a triangle with ∠ BAC = 60 degrees.

Let Γ be incircle of triangle ABC.

Let D , E , F be points of intersection of incircle with sides BC , CA and

AB respectively.

AE = AF , BD = BF , CD = CE.

Let AE = AF = x.

Therefore , AB = x + 3 , AC = x +4 , BD = 3 , DC = 4.

From cosine rule ,

Cos A = ( Sqr(AB) + Sqr(AC) - Sqr(BC) ) / 2 * AB * AC

( Sqr (x) = x * x )

=> Cos 60 = ( Sqr(x+3) + Sqr(x+4) - Sqr (7) )/ 2 * (x+3) * (x+4)

=> 0.5 * 2 * ( Sqr(x) +7x +12 ) = 2 * Sqr (x) + 14x +25 - 49

=> Sqr(x) +7x +12 = 2*Sqr(x) +14x +- 24

=> Sqr(x) + 7x - 36 = 0

Therefore , x = ( - 7 + Root( Sqr(7) - 4 * 1 * (-36)) ) / 2*1

( Eg.Root(49) = 7 )

x = ( -7 + Root(193) ) / 2

Therefore , AB = x + 3 = ( Root(193) - 1 ) / 2

                AC = x + 4 = ( Root(193) + 1 ) / 2

So , Area of triangle ABC = (1/2) * AB * AC * Sin60

= (0.5) * (( Root(193) - 1 ) / 2) * (( Root(193) + 1 ) / 2) * Sin60

= (0.5) * (( Sqr(Root(193)) -1) / 4) * Sin60

=((193-1)/8) * Sin60

=(192/8) * Sin60

=(24) * Sin60

Therefore ,

Sqr(Area of Triangle ABC) = Sqr( 24* Sin60 )

                                           = 576 * Sqr(Root(3)/2)

                                           = 576 * 3 / 4 

                                           = 144 * 3

                                           = 432 .

7r/(12-r^2)=sqrt(3), S=r(sqrt(3)r+7)=12sqrt(3)

The first important thing to note is that the intersections of an incircle split sides $AB, BC,$ and $AC$ into lengths of $x$ and $y, y$ and $z$ , and $x$ and $z$ , respectively. Let $E$ be the intersection of the incircle and side $AB$ , and let $F$ be the intersection of the incircle on side $AC$ . Thus, $EB = ED = 3, DC = FC = 4,$ and $AE = AF.$

Next, using the information that the incircle is formed by the angle bisectors and that $\angle BAC = 60 ^ \circ$ , we get that $AE = AF = r \sqrt{3}$ .

With this information, we can set up two equations to find the area and equate them together, namely that $A = sr = \sqrt{s(s - a)(s - b)(s - c)}$ , where $s$ is the semiperimeter. Substituting in the appropriate values for $s, a, b,$ and $c$ and solving for $r$ , we come to $r = \frac {\sqrt {193} - 7}{2 \sqrt {3}}$ . Substituting this value of r back into either of the equations to find Area and squaring we come to the surprisingly clean number of 432 , our final answer.

Solution 1: Let the distance from $A$ to the circle be $y$ . Applying cosine rule to $\angle BAC$ , we get that $\cos 60^\circ = \frac{ (y+3)^2 + (y+4)^2 - 7^2} { 2 (y+3)(y+4) }$ , or that $y = \frac { -7 + \sqrt{193} } {2}$ (ignore negative root).

This allows us to calculate the area using the sine rule formula, giving

$[ABC] = \frac{1}{2} (y+3)(y+4) \sin 60^\circ = \frac{1}{2} \cdot \frac{ \sqrt{193}-1} {2} \cdot \frac{\sqrt{193} + 1} {2} \cdot \frac{ \sqrt{3} }{2} = \frac{ 192 \sqrt{3} } {16}.$

Thus, $[ABC]^2 = 432$ .

Solution 2: We will use various formulas for the geometric measurements.

Let the corresponding lengths of the triangle are $a, b, c$ , and the corresponding angles be $\alpha, \beta, \gamma$ .
The semi perimeter is $\frac{a+b+c}{2}$ .
Heron's formula states that $[ABC] = \sqrt{ s (s-a) (s-b) (s-c) }$ .
The radius of the incircle is $r = \frac{ [ABC] } { s } = \sqrt{ \frac{(s-a)(s-b)(s-c) } { s} }$ .
Let $E$ be the tangent between $\Gamma$ and $AC$ .
We have $BD = s-c$ , $CD = s-b$ and $AE = s-a$ .
Then $\tan { \frac{\alpha} {2} } = \frac{ r} { AE} = \sqrt{ \frac { (s-b)(s-c) } { s (s-a) } }$ .

Hence, we can calculate that $[ABC] = \frac{ (s-b)(s-c) } { \tan \frac{ \alpha} { 2} } = { 3 \times 4 \times \sqrt{3} } .$ Hence $[ABC] ^2 = 432$ .