This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
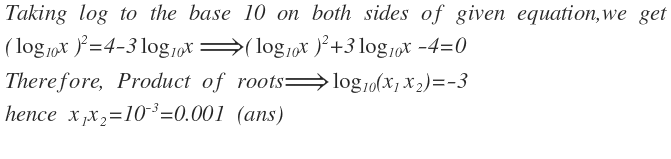
can you simplify for me last 2 lines? where x1 and x2 came from? as there is only x . and log10(x1 x2)=-3 how did that come? plz rply me!
first, multiply bot sides with x 3 x l o g 1 0 ( x ) + 3 = 1 0 4 take log in base x in both sides l o g 1 0 ( x ) + 3 = l o g x ( 1 0 4 ) now, change the base of log l o g x ( 1 0 4 ) = l o g 1 0 ( x ) l o g 1 0 ( 1 0 4 ) = l o g 1 0 ( x ) 4 puting the value in the original equation, we get, l o g 1 0 ( x ) + 3 = l o g 1 0 ( x ) 4 let l o g 1 0 ( x ) = z z + 3 = z 4 ⟶ z 2 + 3 z − 4 = 0 ⟶ z = 1 , 3 since l o g 1 0 ( x ) = z l o g 1 0 ( x ) = 1 , 3 ⟶ x = 1 0 , 3 0
-
Lets take log to the base 10 on both sides of the equation. The result will be:
[ l o g ( x ) ] 2 = − 3 l o g ( x ) + 4 . [ l o g ( x ) ] 2 + 3 l o g ( x ) − 4 = 0 . - Now, lets assume l o g ( x ) = Y .
- As you see, we have a second degree equation Y 2 + 3 Y − 4 = 0 .
-
Solving with Bhaskara's, we have:
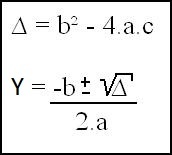
-
Replacing terms, we find {Y¹ = 1 and {Y² = -4 .
-
Afterwards, we have {log(x) = 1 => x = 10^{1} and {log(x) = -4 => x = 10^{-4} .
- Multipling x¹ and x² , we have the product of the roots of the equation is 1 0 1 × 1 0 − 4 = 1 0 − 3 = 0 . 0 0 1 .