Interesting Parallelogram

Geometry Level 4

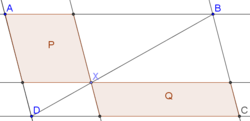
A point $X$ is drawn on the diagonal of a parallelogram $ABCD$ . The lines parallel to the sides through $X$ are constructed, and quadrilaterals $P$ and $Q$ are formed, as shown in the diagram.

Given that $Q$ has base $12$ and perpendicular height $4$ and that the area of $ABCD$ is $200$ , find the sum of all possible values of the base of $P$ .

The answer is 26.

1 solution

Michael Ng
Oct 22, 2014

By considering congruent triangles we see that the area of P is equal to the area of Q so P has area 48. Then we can form the equations (where $b$ and $h$ are the base and perpendicular height respectively of P):

$bh=48$

$(b+12)(h+4)=200$

Then:

$12h+4b=104$

$144+b^2=26b$

$(b-18)(b-8)=0$

$b=18, 8$

So the answer is $\boxed{26}$

Interesting Parallelogram

The answer is 26.

1 solution

0 pending reports