Interference of a photon with itself
Consider the following setup for an interferometer:
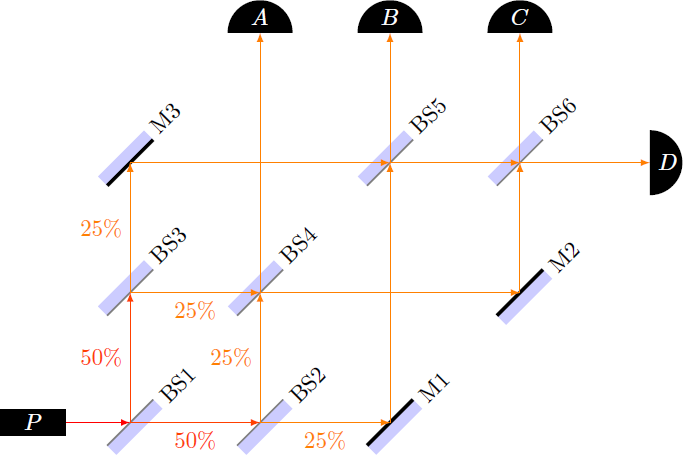
The optical setup consists of
- One photon emitter (P)
- Six beam splitters (BS1, BS2, BS3, BS4, BS5 and BS6)
- Three mirrors (M1, M2 and M3)
- Four detectors (A, B, C and D)
The photon emitter produces a single photon, that travels through the interferometer. What is the probability that this photon will be detected at point D?
Assumptions:
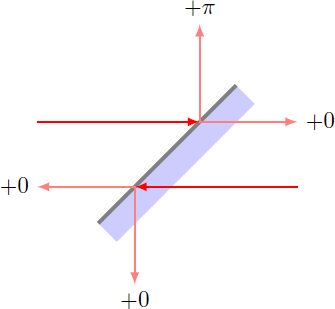
- There is no scattering and absorption in the interferometer, so that no photon is lost when passing through the optics. All mirrors have 100% reflectivity and the detectors are 100% efficient. Each photon that passes through the interferometer is detected at exactly one of the four detectors.
- The beam splitters consisted of a glass plate with a thin, reflective dielectric layer on the front. The reflected light from the front side undergoes a phase shift by (corresponds to ), while in the reflection at the back no phase shift occurs. Even with transmission along both directions, the phase of the light remains unchanged. All beam splitters divide the light into two partial beams of the same intensity.
- All optical components are perfectly adjusted, so that partial beams in BS4, BS5 and BS6 are reunited at the same point and have traveled the same optical path (except for the phase shifts in reflection).
Bonus question: What would change, if a light absorber is placed between M1 and BS5, so that this partial beam is completely blocked?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If we track all beam intensities and phase shifts along the possible paths, we get the following result
At the points BS4, BS5 and BS6 we have to consider the interference of two partial beams of the same intensity. We get a perfect destructive interference, if the phase shifts of the partial beams differ by ± π , and a perfect constructive interference, if the phases are the same. As it turns out, the photon can only be detected at point D, because the other rays are extinguished by interference.
The confusing thing is that only a single photon passes through the interferometer. Thus, the particle would have to complete several paths simultaneously and to interfere with itself. From the point of view of classical physics, this is completely impossible, since a particle can only ever stay in one particular place at a certain time. Thus, this experiment can only be understood from the perspective of quantum mechanics.
It becomes even more interesting when the absorber is placed in the beam path, so we get the following result:
In contrast to the previous experiment, the photon can also be observed at points B and C with the probabilities of 12.5% and 6.25%, respectively, as there is no longer any interference or only a partial extinguishing of the rays. If, therefore, the photon is observed at B or C, then the presence of an absorber in the beam path has been confirmed experimentally because this measurement result was previously impossible. Thus there is a chance to optically detect the absorber without ever absorbing a photon (interaction-free measurement).
This interferometer is a modification of the Elitzur–Vaidman bomb tester , whereby in contrast to the original construction, there is an increased chance of 43% instead of 33% to detect a light-sensitive bomb without this is ignited. More puzzles of this kind can also be found here .