Interference on a cylindrical screen

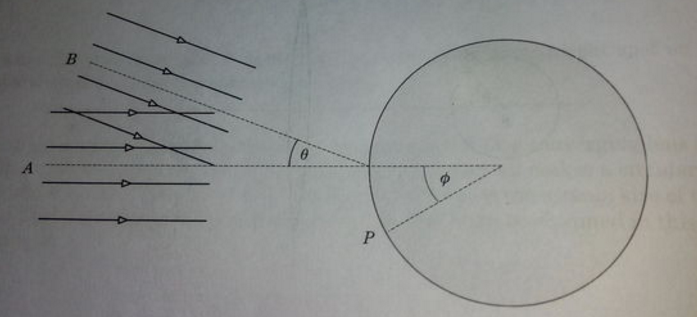
Two identical beams $A$ and $B$ of plane coherent waves of the same intensity and wavelength $\lambda$ on a cylindrical screen. The angle between the directions of the beam propagations is $\theta$ . Consider a point $P$ on the screen at angular position $\phi$ from the beam $A$ as shown in the figure. Find distance between adjacent interference fringes on the screen near the point $P$ . Assume that the distance $\beta$ between adjacent fringes is much less than the radius of the cylinder.

If $\sin \left ( \dfrac\theta2 \right) \cos \left( \dfrac \theta2 + \dfrac \phi 2 \right) = \dfrac \lambda 2$ . Find the fringe width at point $P$ on the cylindrical screen.