Intern at the Laborious Laboratory

First of all, let's convert the fractions $\frac{1}{3}$ , $\frac{1}{4}$ , and $\frac{1}{5}$ to $\frac{20}{60}$ , $\frac{15}{60}$ , and $\frac{12}{60}$ . Since the desired amount of hydrochloric acid is $\frac{1}{60}$ , we can scale the unit of measure down buy a factor of 60 (1/60 liter = 1 unit) which enables us to work with only integers.

When modeling the procedure, I use the format (12 unit flask, 15 unit flask, 20 unit flask) to denote the amount of HCl in each flask at any given step in the procedure.

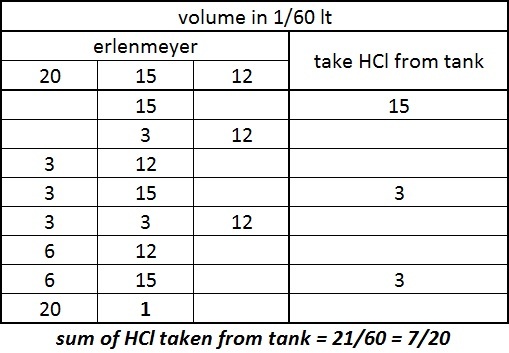
So we have flasks of $20$ , $15$ ,and $12$ units, and we want to measure $1$ unit. Since we are careful, we start by filling the 15 unit flask. However, filling the 15 unit flask only allows for us to measure shifted variations of $(0,15,0)$ and $(12,3,0)$ , so clearly 15 units -- and anything less -- doesn't give the intern enough flexibility to measure out 1 unit of HCl.

However, if we use our 15 units to achieve the setup $(0,12,3)$ , we can add 3 units to fill up the 15 unit flask, and we get $(0,15,3)$ . 18 total units of HCl allows for much more transfer options than 15 units, yet even so, none of the possibilities using only 18 units involve a flask having a non-multiple of 3 amount of HCl. So 18 units isn't enough, and in fact anything less than 20 units only allows the intern to measure 3*x units of HCl.

So let's try 20 units of HCl. Note that $(0,0,20)$ must be the initial setup if your last move was to increase the amount of HCl to 20 units. With that in mind, let's see what happens:

$(0,0,20)$ $(0,15,5)$ $(12,3,5)$ $(0,3,17)$ $(3,0,17)$ $(3,15,2)$ $(12,6,2)$ $(0,6,14)$

At this point, it is impossible to make another transfer without quickly leading to one of the previous steps, so 20 units is still not enough. However, we can do the following:

$(0,6,14)$ $(6,0,14)$ $(6,14,0)$ $(6,15,0)$

In that last step, we added 1 unit to fill up the 15 unit flask. Look at what happens next!

$(6,15,0)$ $(6,0,15)$ $(1,0,20)$

So 21 units, as it turns out, is all we need to measure 1 unit of HCl! Since anything less does not work, 21 units is the minimum . 21 units = 21/60 liters = $\boxed{\frac{7}{20}}$