International Mathematical Olympiad (IMO) , Day , Problem of
An anti-Pascal triangle is an equilateral triangular array of numbers such that, except for the numbers in the bottom row, each number is the absolute value of the difference of the two numbers immediately below it. For example, the following array is an anti-Pascal triangle with four rows which contains every integer from to .
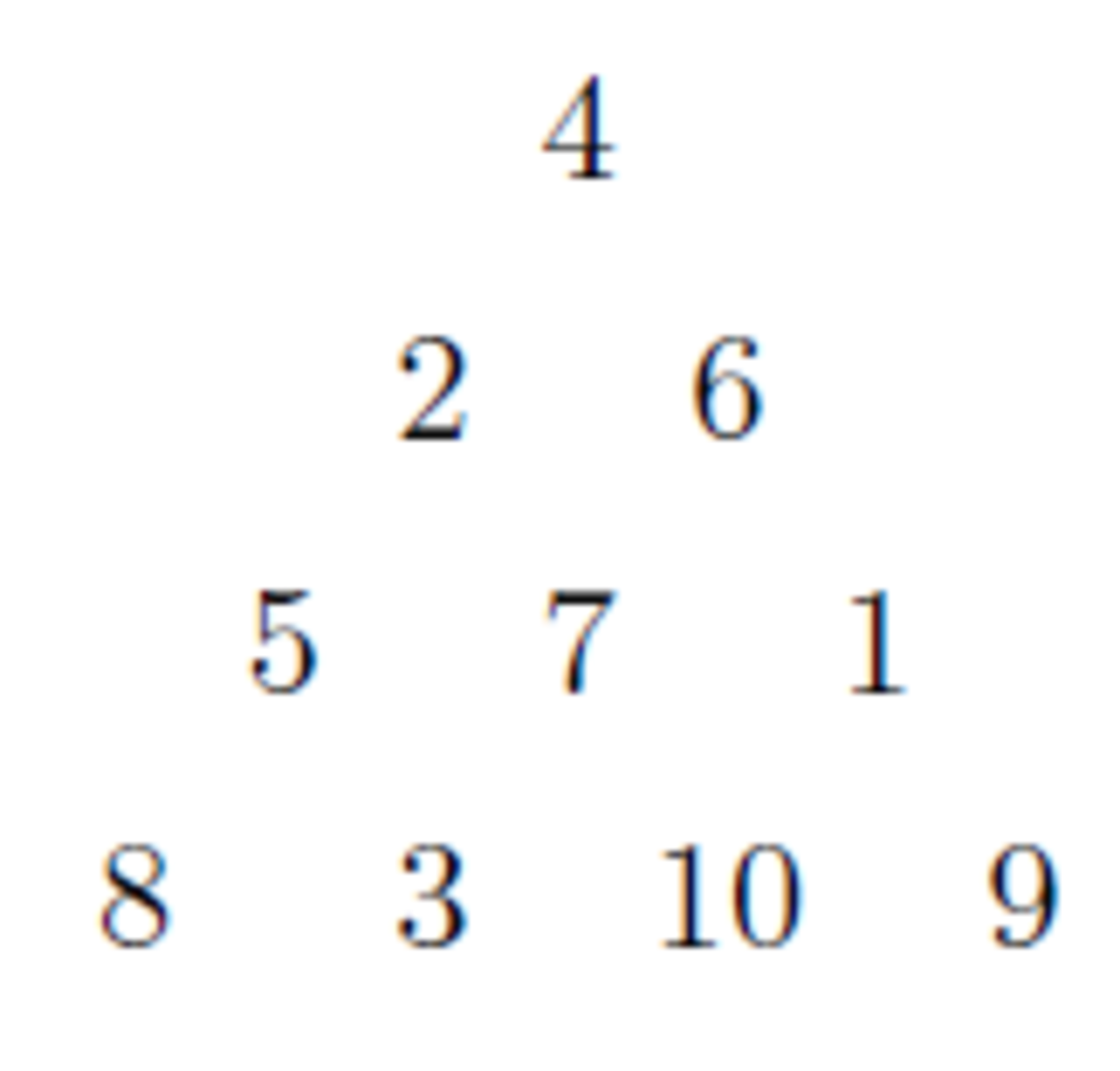
Does there exist an anti-Pascal triangle with 2018 rows which contains every integer from to ?
The person who answers this correctly and gives the official solution first - there is - go to International Mathematical Olympiad (IMO) Hall of Fame
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For any number not in the bottom row (let us name it d for easy use) draw a line from d to the larger number which is directly below it (there should be two numbers below a number) This will form a shape that looks like a lightning strike (it looks cool, try it yourself with a large anti-Pascal!)
Consider the directed path starting from the top vertex A . Starting from the first number, it increases by at least 1 + 2 + ⋅ ⋅ ⋅ + n , since the increases at each step in the path are distinct; therefore equality must hold and thus the path from the top ends at N = 1 + 2 + ⋅ ⋅ ⋅ + n with all the numbers 1 , 2 , . . . , n being close by. Let B be that position.
Consider the two left/right neighbors X and Y of the endpoint B. Assume that B is to the right of the midpoint of the bottom side, and complete the equilateral triangle as shown to an apex C. Consider the lightning strike from C hitting the bottom at D.
It travels at least ( f l o o r ) n / 2 − 1 steps, by construction. But the increases must be at least n + 1 , n + 2 , . . . since 1 , 2 , . . . , n are close to the A → B lightning path. Then the number at D is at least ( n + 1 ) + ( n + 2 ) + ⋅ ⋅ ⋅ + ( n + ( b n / 2 − 1 c ) ) > 1 + 2 + ⋅ ⋅ ⋅ + n
for n ≥ 2 0 1 8 , a contradiction occurs.