International Mathematical Olympiad (IMO) , Day , Problem of
Question:
A social network has users, some pairs of whom are friends. Whenever User A is friends with User B, User B is also friends with User A. Events of the following kind may happen repeatedly, one at a time:
Three users A, B, and C such that A is friends with both B and C, but B and C are not friends, change their friendship statuses such that B and C are now friends, but A is no longer friends with B, and no longer friends with C. All other friendship statuses are unchanged.
Initially, users have friends each, and users have friends each. Prove that there exists a sequence of such events after which each user is friends with at most one other user.
Country that gave the Question: Croatia
The person that answers correctly and gives the official solution first - there is , go to International Mathematical Olympiad (IMO) Hall of Fame
Note - For this question, enter if it's correct (i.e. it can be proved) or if it's incorrect (i.e. it cannot be proved).
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Solution 1 :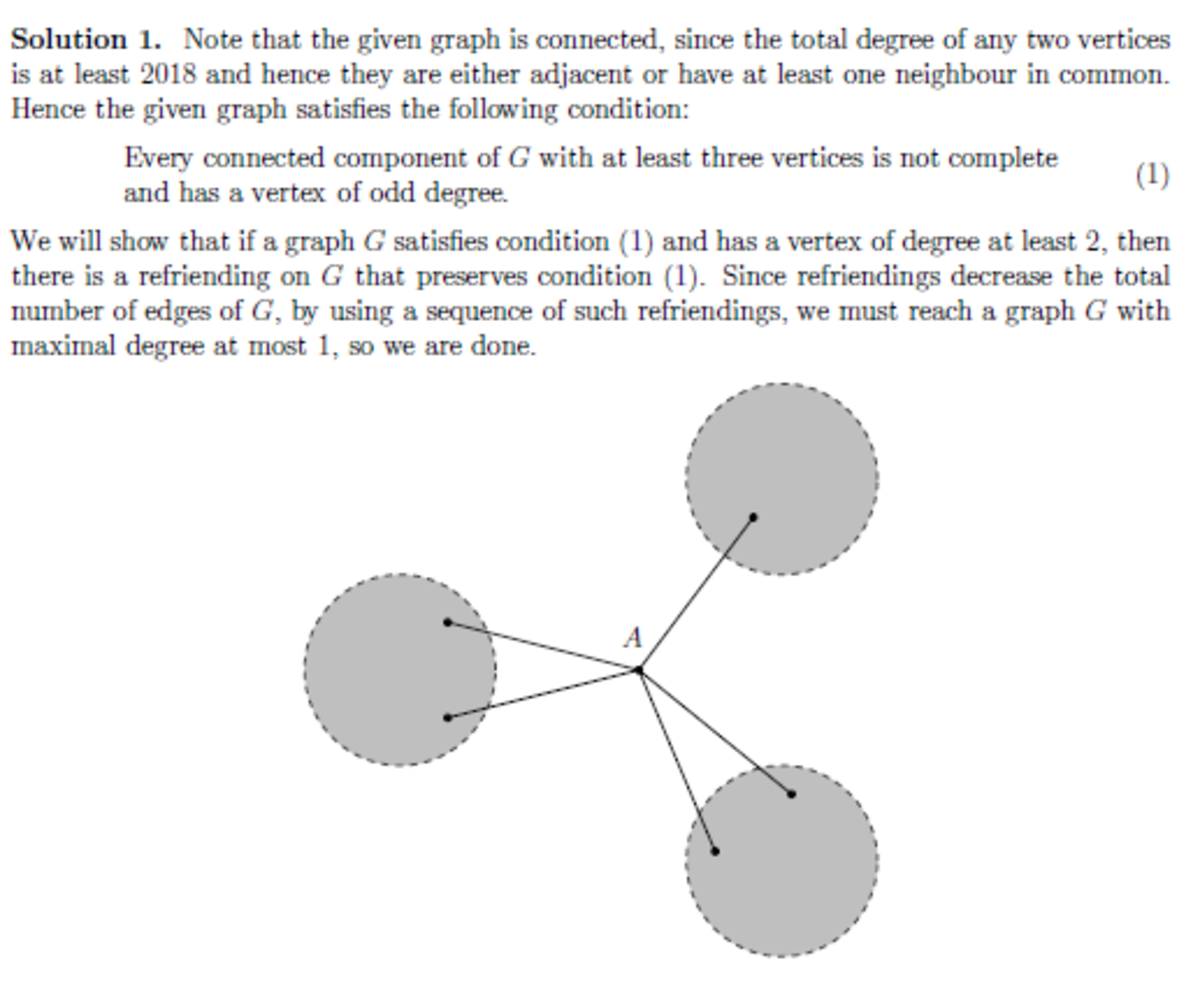
 Solution
2
:
Solution
2
:
