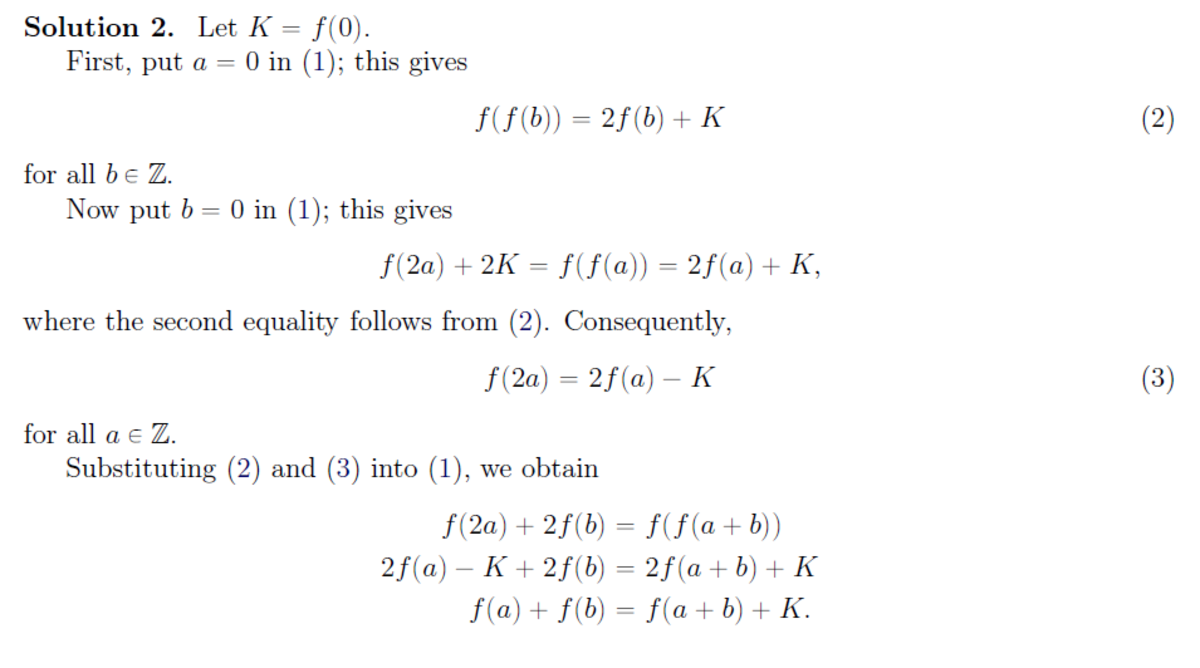International Mathematical Olympiad (IMO) 2 0 1 9 , Day 1 , Problem 1 of 6
Question:
Let Z be the set of integers. Determine all functions f : Z → Z such that, for all integers a and b ,
f ( 2 a ) + 2 f ( b ) = f ( f ( a + b ) )
Country that gave the Question: South Africa
The person that answers this correctly and gives the official solution first - there is 2 - go to International Mathematical Olympiad (IMO) Hall of Fame
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Same way as the first solution.
Log in to reply
No, it has to be the entire official solution...
Let us examine two Cases:
CASE I ( f is constant): This yields C + 2 C = C ⇒ 2 C = 0 ⇒ C = 0 . Hence, f ( n ) = 0 is the only constant solution for all n ∈ Z .
CASE II ( f is non-constant): The function f ( n ) is linear in order to preserve the mapping of this Cauchy functional equation (i.e. f ( n ) = A n + B for A , B ∈ Z . ) Substituting this linear expression into the original equation above yields:
[ A ( 2 a ) + B ] + 2 [ A ( b ) + B ] = A [ A ( a + b ) + B ] + B ;
or 2 A a + 3 B + 2 A b = A 2 a + A 2 b + ( A + 1 ) B .
If 2 A = A 2 , then A = 0 , 2 . For A = 0 ⇒ 3 B = B ⇒ B = 0 , which corroborates with Case I above. For A = 2 ⇒ 4 a + 3 B + 4 b = 4 a + 4 b + 3 B ⇒ B = K , where K is any integer. Thus, f ( n ) = 2 n + K is the family of solutions that satisfies non-constant f .
Nice solution! I'll check if it's the official one, @Tom Engelsman
@Tom Engelsman , you have not got the official solution...
But, great work! I can see you have bits of it.
Log in to reply
Thanks, Yajat…..not bad for a midnite Brilliant binge ;)
Solution 1 : Solution
2
:
Solution
2
: