International Physics Online Olympiad 2014
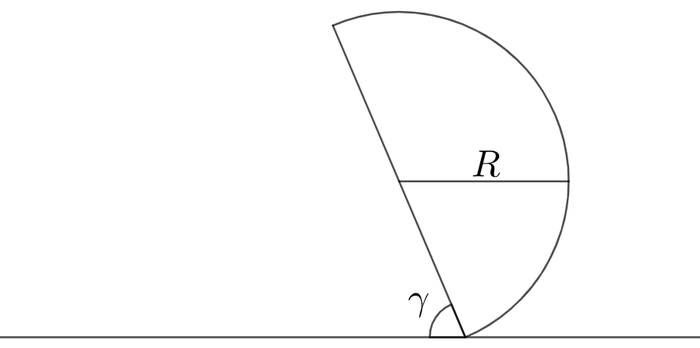
A uniform solid semi-circular disk of radius R and negligible thickness rests on its diameter. As shown above, it is then tipped over by some angle γ with respect to the table. At what minimum angle will the disk lose balance and tumble over? Express your answer in degrees, rounded to the nearest two decimal places.
The answer is 67.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Amazing solution; recently I have been revisiting pen and paper physics problems. This one is quite nice, well done sir.
I think you meant X C = 2 R because the disk has a line of symmetry given by x = 2 R . Using the integral X C = ∫ 0 R σ R 2 − ( x − 2 R ) 2 d x ∫ o R σ x R 2 − ( x − 2 R ) 2 d x also gives the same result. So γ = 2 π − tan − 1 ( 3 π 8 ) .
Log in to reply
Nice catch. I realise that I made a mistake in my diagrams. The coordinate of the point initially on the X axis is ( 2 R , 0 ) and not ( R , 0 ) .
Consider a uniform semi-circular disk as shown in the diagram. To compute the X and Y coordinates of the COM of this uniform semi-circular disk, the following two relations are used. Let the mass per unit area be σ .
X C = ∫ A d m ∫ A x d m = ∫ 0 π ∫ 0 R σ r d r d θ ∫ 0 π ∫ 0 R ( R + r cos θ ) ( σ r d r d θ ) = R Y C = ∫ A d m ∫ A y d m = ∫ 0 π ∫ 0 R σ r d r d θ ∫ 0 π ∫ 0 R ( r sin θ ) ( σ r d r d θ ) = 3 π 4 R
Having found the COM coordinates, imagine that the disk is rotated about the Z-axis such that the point on it coincident with the origin is fixed. If it is rotated anti-clockwise by a small angle, it is expected to return to its original position due to the component of weight that brings it back down.
One can see that the net unbalanced torque about the origin in the clockwise direction brings it back to its initial orientation. The only way that the disk can tip over is when the angle is increased so that the weight is to the left of the reaction force. The point at which the disk just tips over is when the weight and reaction forces are aligned. This happens when the COM intersects the Y-axis. In other words, the disk must be rotated by an angle so that the COM lies exactly on the Y axis. Let the initial position vector of the COM be:
r = X C i ^ + Y C j ^
The angle this vector makes with the horizontal is:
α = arctan ( X C Y C ) = arctan ( 3 π 4 )
Therefore the angle by which the disk must be rotated is:
γ = 2 π − α = 2 π − arctan ( 3 π 4 )
γ ≈ 6 7 ∘