Intersectception
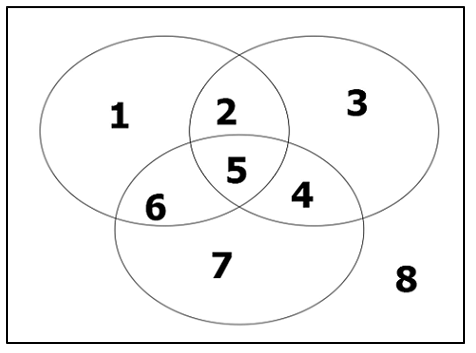 Above shows an illustration of 3 circles the divide the plane into 8 regions with the properties that two circle intersect in two points and no three of the circles pass through the same point.
Above shows an illustration of 3 circles the divide the plane into 8 regions with the properties that two circle intersect in two points and no three of the circles pass through the same point.
Can you find the maximum number of regions into which 10 circles divide the plane?
The answer is 92.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There would be n × ( n − 1 ) intersections to n circles. These will create n × ( n − 1 ) distinct areas, excluding the portion common to all the n circles and also excluding the exterior.
Therefore, a 1 0 = 1 0 × 9 + 2 9 2