Intersecting Circles

Geometry Level 2

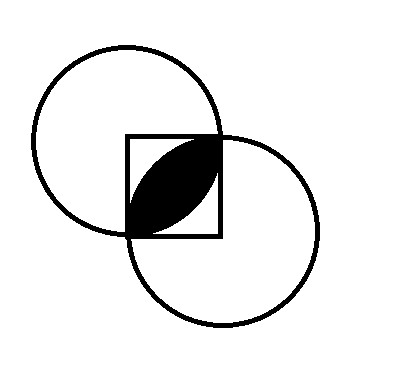A square with side length of 5 is drawn. Using a vertex of the square as the center and the square's side length as its radius, a circle is drawn. Using the vertex diagonally opposite of the one we just used as the center and the square's side length as its radius, another circle is drawn. Find the area of the intersection between the two circles.

6.25 π + 25 6.25\pi+25 12.5 π − 25 12.5\pi-25 12.5 π + 25 12.5\pi+25 − 12.5 π − 50 -12.5\pi-50 − 12.5 π + 50 -12.5\pi+50 − 6.25 π + 50 -6.25\pi+50 6.25 π − 25 6.25\pi-25 − 6.25 π − 50 -6.25\pi-50

View wiki
Austin Cheng by Austin Cheng , 20, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Farhan Abir
Apr 18, 2015

In figure 'a' it showed the problem. In figure 'b' it showed how we can deduce the area. If we take the half of the intersected area, we can find something like figure b. here, 1/4th of the circle having a radius of 5 is cut by a cord(diagonal of square). so the area of that part will be:

Area of 1/4th of the circle - Area of right angled triangle formed by two sides of square and chord. = (1/4 x 25π) - (1/2 x 5 x 5) = 6.25π - 12.5

so, the two parts will combine. so the total are will be: 2 x (6.25π - 12.5) or, 12.5π-25

so, Answer is: 12.5π -25

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Pankaj Munjal
Jun 18, 2015

Let us consider the area of dark portion be made by: area of sector from first circle+ area of sector from second cirle - area of square Area of sector from frst circle: πr^2/4 i.e π25/4 Area of sector from second circle: π25/4 Area of square: r^2 i.e 25 Therefore, area of dark portion= π25/4 + π25/4 - 25 = 12.5π - 25

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...