Intersecting Pyramids Edited
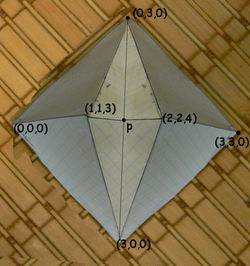
Two pyramids with 3 cm. square bases intersect. Their bases have the coordinates of (0,0,0), (3,0,0), (3,3,0) and (0,3,0). The pinnacle of one is at (1,1,3) and of the other is (2,2,4). The highest point of intersection is P(x,y,z). Calculate x + y + z to nearest 3 decimal places.
The answer is 5.143.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider the line between (0,0,0) and (3,3,0). Both pinnacles are above this line. P must lie above this line since if it were not, we could make it higher by moving it closer. So P has coordinates (x,x,z).
If you draw a sketch of the vertical cross-section intersecting the line, you see that there are 3 points where the pyramids intersect, and the highest is in the middle, where 1<x<2. The coordinates satisfy z=3/2*(3-x) (since P is on the 1st pyramid), and z=2x (since P is on the 2nd pyramid).
Solving yields x=9/7, so y=9/7 and z=18/7.