Intersecting Squares and Circles

Right, so let 2r = R, and s = S. Simon chooses an interval of length S, and Rachel chooses an interval of length R. We want to determine the probability that the intervals intersect. Let's assume that R + S < 33, since otherwise that probability is 1.

So if Simon chooses first, he picks a real number, x in [0,33 - S] to be the left endpoint of his interval. Then, Rachel selects a real number in [0,33 - R]. The intervals intersect iff Rachel's is in [x-R, x + S - R], and so the probability of this happening is:

1/(33-R) * (min(33 - R, x + S - R) - max(0, x - R))

We want to integrate this over all possibilities for x. Note that x has uniform distribution, so the integral we're calculating is:

1/(33-R)(33-S) * integral from 0 to (33-S) of (min(33 - R, x + S - R) - max(0, x - R)).

I'll leave out the details, but what we do from here is separate the min and max integrals, translate the min integral so it's (33 - R) + min(0, x + S - 33), substitute to get min(0,y) and max(0,z), reflect the min integral and notice that the limits are the same to get:

1 - 2/(33-R)(33-S) * integral from -R to (33 - S - R) of max(0,z) dz.

We ignore the part of the integral to 0, and recall that S + R < 33 to obtain an equation in R and S that we want to solve:

2(33 - S - R)^2 = (33 - S)(33 - R).

Now, R is even, so S must be odd as LHS is even. Hence, 33 - S - R is even and so 33 - S is divisible by 8. One way to finish from here is to solve the four quadratic equations you get for S = 1,9,17,25 and notice that (R,S) = (6,9) is the only one that works, giving an answer of 12.

For the circle and the square to intersect, they must intersect at a point along the interval, since if they have a point of intersection at $(m,n)$ then they also have an intersection at $(m,0)$ .

Let $x$ be the leftmost point of the interval of length $2r$ and $y$ the leftmost point of the interval with length $s$ . We have the inequalities $0 \leq x \leq 33 - 2r$ and $0 \leq y \leq 33 - s$ , and $x,y$ are randomly distributed along these intervals. In order for the intervals to intersect, we need to have $y - x \leq 2r$ and $x - y \leq s$ . We graph these in the figure below

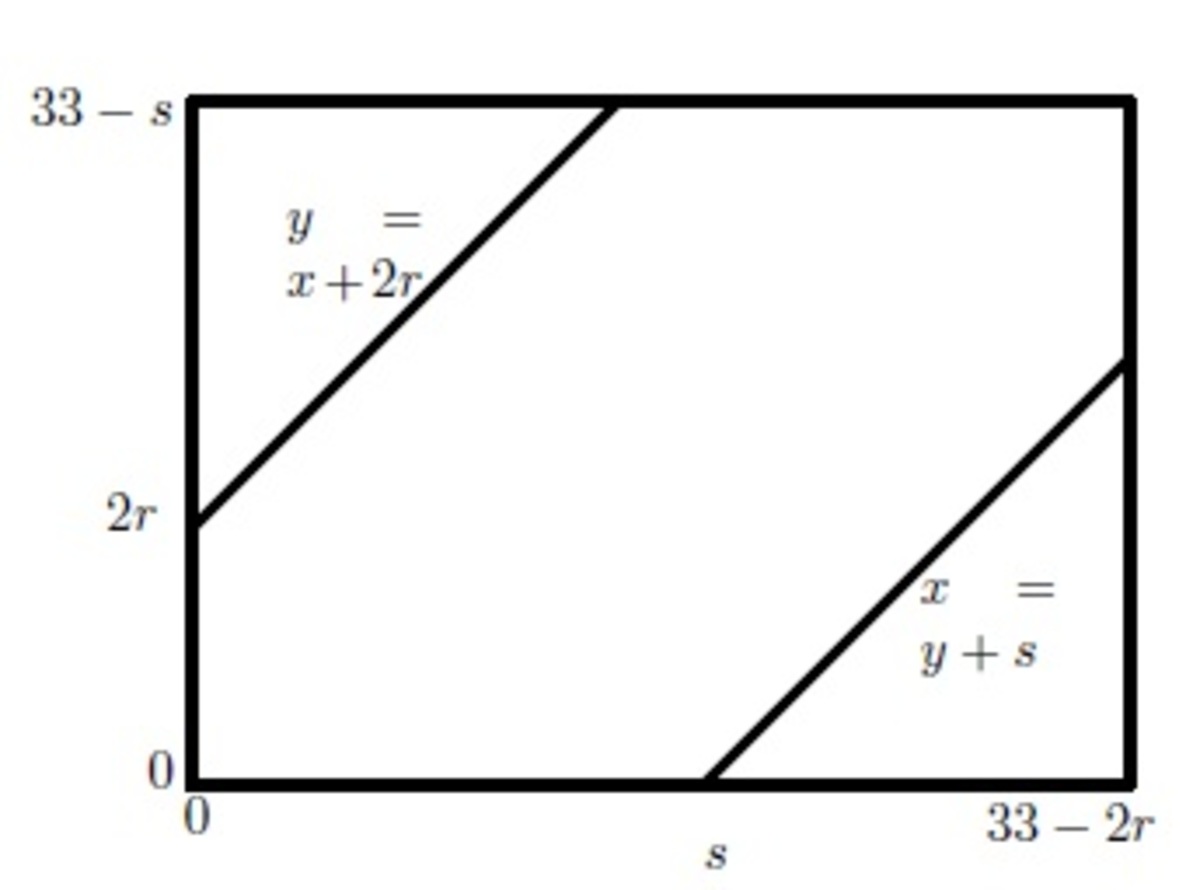
The interior region is the set of points where both inequalities are satisfied, and so these are the points where the segments will intersect. The two outer triangles each have both their side lengths $33 - s - 2r$ , so the sum of their areas is $(33-s-2r)^2$ , and the area of the whole region is $(33 -s)(33-2r)$ . In order for the probability that the segments intersect to be $\frac{1}{2}$ , we must have $\frac{(33-s-2r)^2}{(33-s)(33-2r)} = \frac{1}{2}$ .

We examine the numerator and denominator of the LHS of this equation. Since $r$ and $s$ are both integers, the numerator and denominator must be integers, such the the denominator is twice the numerator. Since 2 divides the denominator, we must have $33-s$ is even, and so $s$ is odd. Having $s$ odd means that $(33-s-2r)$ is also even, and so we must have $8 \mid (33-s)$ . This gives $s = 1, 9, 17, 25, 33$ as possible solutions.

Note that $33-s-2r$ must be positive. [In fact, we have further restrictions. We cannot have $s \geq 17$ , since then for any positive $r$ value the probability that they intersect will be greater than a half, because the segment of length $s$ would cover over half the interval $[0,33]$ . Likewise, we cannot have $r \geq 9$ , since for any positive $s$ value, the probability that they will intersect is greater than a half because the segment of length $2r$ would cover over half the interval $[0, 33]$ .

If $s = 1$ , we have $\frac{(32 - 2r)^2}{32(33-r)} = \frac{1}{2}$ or equivalently $(32-2r)^2 = 16(33-2r)$ . This has solutions $12 \pm 2\sqrt{5}$ which are not integers.
If $s = 9$ , we have $\frac{(24 - 2r)^2}{24(33-2r)} = \frac{1}{2}$ . This quadratic equation is $0=4r^2 - 72r + 180= 4(r-3)(r-15)$ . If $r=15$ , this contradicts $33-s-2r > 0$ and $r \leq 9$ . If $r=3$ , we see that $33 - s - 2r = 18$ is positive, and our answer is valid.

Thus, the only solution is $s = 9, r = 3$ so $\sum\limits_{(s,r) \in S} (s + r) = 9 + 3 = 12.$