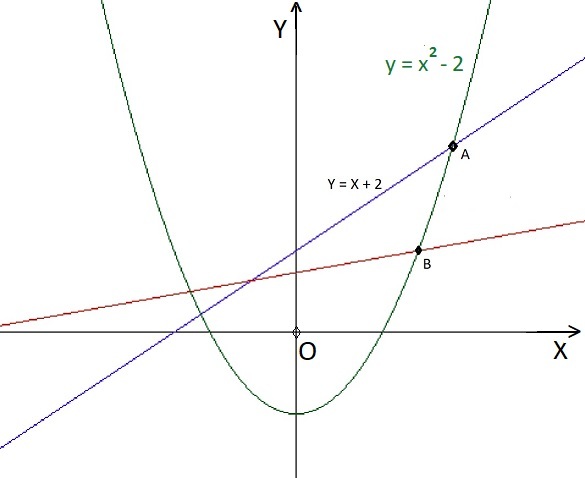
Intersection after rotation

Since $y = x + 2$ rotates $30°$ around the origin, we can apply the rotation formulas $x' = x \cos \theta - y \sin \theta$ and $y' = x \sin \theta + y \cos \theta$ to find the new rotated line equation $x \sin 30° + y \cos 30° = x \cos 30° - y \sin 30° + 2$ which simplifies to $y = (2 - \sqrt{3})x + 2(\sqrt{3} - 1)$ .

Then the intersection at $B$ occurs when $y = (2 - \sqrt{3})x + 2(\sqrt{3} - 1) = x^2 - 2$ , and so $x^2 - (2 - \sqrt{3})x - 2\sqrt{3} = 0$ or $(x - 2)(x + \sqrt{3}) = 0$ , which means $x = 2$ or $x = -\sqrt{3}$ . Since the point of intersection is to the right of the origin, $x = 2$ , and so $y = x^2 - 2 = 2^2 - 2 = 2$ , and $\frac{xy}{x + y} = \frac{2 \cdot 2}{2 + 2} = \boxed{1}$ .

When a line is rotated about a point, its distance to the point never changes. It is how we find the equation of the second line.

Let $d_1$ be the distance of the original line from the origin. Using the formula $d=\frac{|c|}{\sqrt{a^2+b^2}}$ to calculate the distance of the line $x-y+2=0$ to the origin $(0,0)$ , we get $d_1=\frac{2}{\sqrt{2}}$ .

Now, because the original line has slope of $1=\tan{(45^{\circ})}$ , and that it was rotated $30^{\circ}$ , then the slope of the second line is $\tan{(15^{\circ})}=2-\sqrt{3}$ .

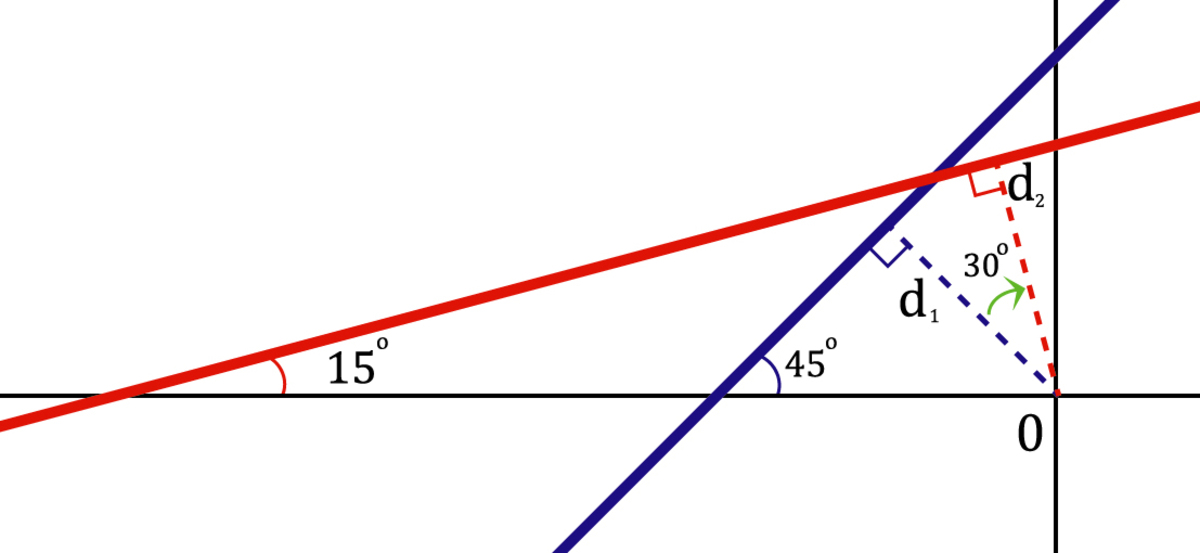
Then, using the the slope-intercept form of a line, the equation of the second line is

$y=(2-\sqrt{3})x+b$ . Since the distance of the second line to the origin is equal to the first distance, that is, $d_1=d_2$ , then, using the formula I earlier mentioned, $d_2 = \frac{|c|}{\sqrt{a^2+b^2}}$

$\frac{2}{\sqrt{2}} = \frac{|b|}{\sqrt{1+(2-\sqrt{3})^2}} = \frac{|b|}{\sqrt{1+4-4\sqrt{3}+3}} = \frac{|b|}{\sqrt{8-4\sqrt{3}}}$

$|b| = \frac{4\sqrt{2-\sqrt{3}}}{\sqrt{2}} = 4\sqrt{1-\frac{\sqrt{3}}{2}} = 4(\frac{\sqrt{3}}{2}-\frac{1}{2}) = 2\sqrt{3} - 2$ .

Therefore, the equation of the second line is

$y = (2-\sqrt{3})x+2\sqrt{3} - 2$ .

As a last step, to solve for the point where the curve $y=x^2-2$ and the second line intersects, we equate them and we solve for the greater value of x, since it is obvious that $B$ has a greater value of $x$ than their other point of intersection.

$(2-\sqrt{3})x+2\sqrt{3} - 2 = x^2-2$

$x^2 - (2-\sqrt{3})x-2\sqrt{3} = (x - 2) (x + \sqrt{3}) = 0$

Since $x_1=2$ is greater than $x_2=-\sqrt{3}$ , then we use $x_1=2$ and plug it in the equation of the curve.

$y=x^2-2=4-2=2$

Therefore, the coordinate of point $B$ is $B(x,y)=B(2,2)$ .

Thus, $\boxed{\frac{x \times y}{x+y}=\frac{4}{4}=1}$ .