Intersection Area of Venn Diagram 2
Two circles with a radius 1 overlap each other. The overlapped area is half of either circle's area. How far apart are the circles' centers into each other?
 Not to scale with given information
Not to scale with given information
NOTE: The answer must be written in the nearest ten-thousandths.
Try Part 1
The answer is 0.8079.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Instead of setting the complicated equation with sin, use x = 2 cos (132.34646/2)
I had a slightly different approach than the other proposed solutions. Let us consider the area subtended by the angle formed by the lines extended from the centre of one of the circles to the points of intersection between the two circles. This is overlap region formed is symmetric, thus we multiply this area by two, and subtract two times the area formed by the triangle formed by the centre of one of the circles, and the two points formed by the intersection of the circles, in order to get the area of the overlap. Let θ be half the subtending angle. We then get:
2 1 π R 2 = 2 [ 2 π 2 θ π R 2 − ( 2 ) 2 1 R 2 cos θ sin θ ] = 2 θ R 2 − 2 R 2 cos θ sin θ = R 2 ( 2 θ − sin 2 θ ) 2 π = 2 θ − sin 2 θ ⇒ sin 2 θ = 2 θ − 2 π
We can solve this numerically, to get θ = 1 . 1 5 5
Now, if we let the distance between the two midpoints be d , we can see that:
d = 2 R cos θ
So we get:
d = 2 ( 1 ) cos 1 . 1 5 5 = 0 . 8 0 7 8 4
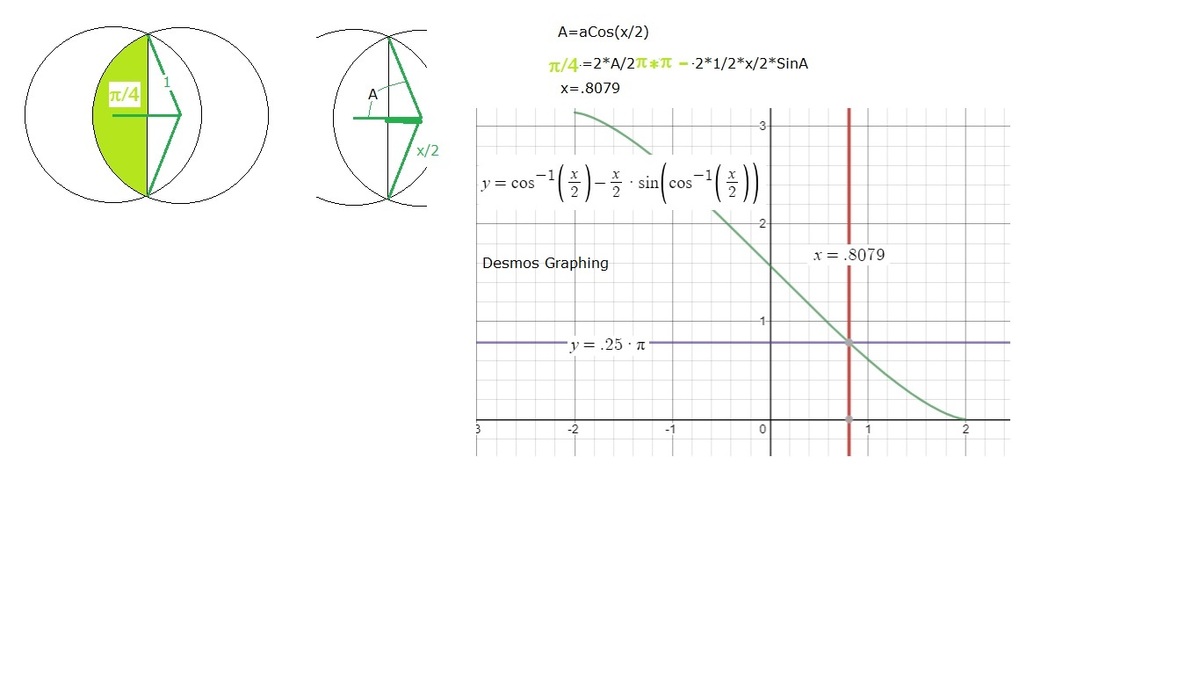
The overlapped area is made up of two segments. Since that area is half the area of either circle, each segment has an area of 4 π . We can now get the central angle of the segments.
3 6 0 π x ° − 2 sin x ° = 4 π
Plugging that in a calculator, we get x ≈ 1 3 2 . 3 4 6 4 6 . Now we can get the length between the circles' centers.
We'll use the Sine rule:
sin ( 1 8 0 − 1 3 2 . 3 4 6 4 6 ) ° x x sin 6 6 . 1 7 3 2 3 ° x x = sin ( 2 1 3 2 . 3 4 6 4 6 ° ) 1 = sin 4 7 . 6 5 3 5 4 ° = sin 6 6 . 1 7 3 2 3 ° sin 4 7 . 6 5 3 5 4 ° = 0 . 8 0 7 9 4 5
The centers are 0 . 8 0 7 9 units apart from each other.