Intersection Area of Venn Diagram
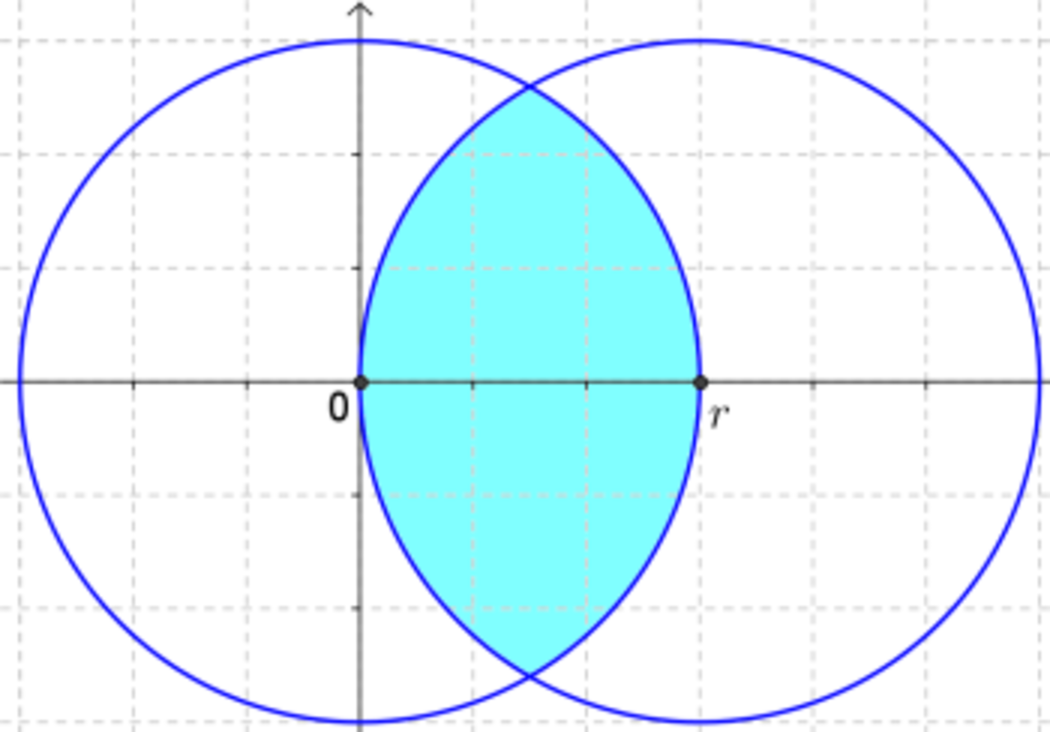
Two circles with the same radius overlap each other. Their circumferences cross each other's center. How much of the area of either circle in percentage is the overlapped area? Give your answer in the nearest tenths.
Try Part 2 .
The answer is 39.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
WLOG r = 1 . Then, we can find the area of the shaded region by 2 ⋅ [ Area of the 1 2 0 ∘ sector ] − [ The two equilateral △ ] . The area of the sectors, since we let r = 1 , is 2 ( 3 1 π ) = 3 2 π . The area of an equilateral triangle is given by 4 3 s 2 , where s is the length of one side, so the area of the two equilateral triangles is 2 ( 4 3 ) = 2 3 . Thus, we have the answer as π 3 2 π − 2 3 ≈ 3 9 . 1 % .
I should have been more clear that it was an 1 2 0 ∘ angle because of the two equilateral triangles.
In the Quadrant I , the arcs cross at 0 . 5 of the x-axis. Using this information, we can get the angle of the circles' segments that make up the overlapped area.
Let's use the Sine Rule:
sin 9 0 ° 1 = 1 = x = sin ( 9 0 − x ) ° 0 . 5 sin ( 9 0 − x ) ° 0 . 5 6 0
We can now get the area of the segment.
3 6 0 1 2 0 ° π − 2 sin 1 2 0 ° = 6 2 π − 4 3 ≈ 0 . 6 1 4 1 8 5
Since there are two identical segments creating the area, we double the result above. The area of each circle is π , so we just divide the two to get our answer.
π 3 2 π − 2 3 ≈ 0 . 3 9 1 0 0 2 or 3 9 . 1 %
If the image doesn't appear, here it is .