Intersection Area
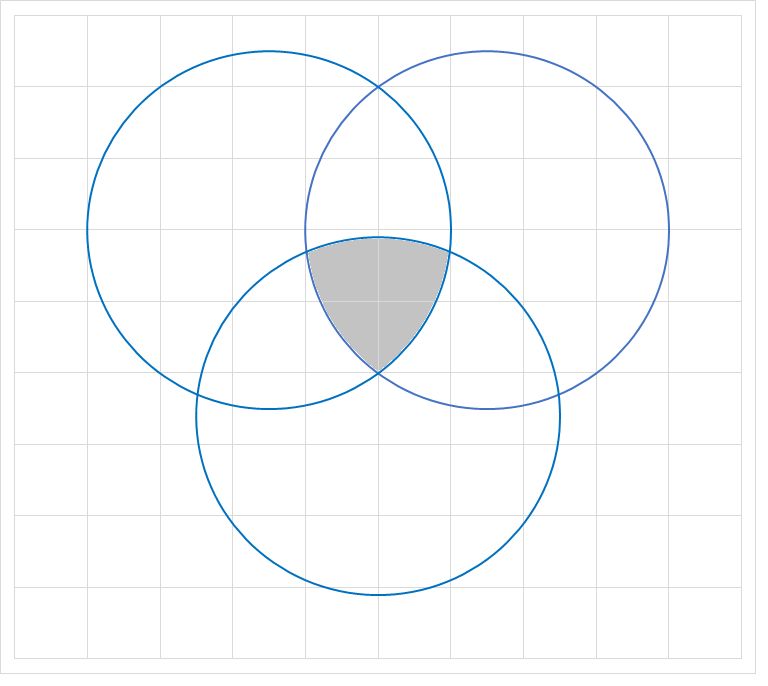
Three circles, each with radius 5 units, are positioned as in the figure above with the distance between any two centers equal to 6 units. Find the area of the intersection region of the three circles (shaded light gray).
Round your answer to 2 decimal places.
The answer is 9.87.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
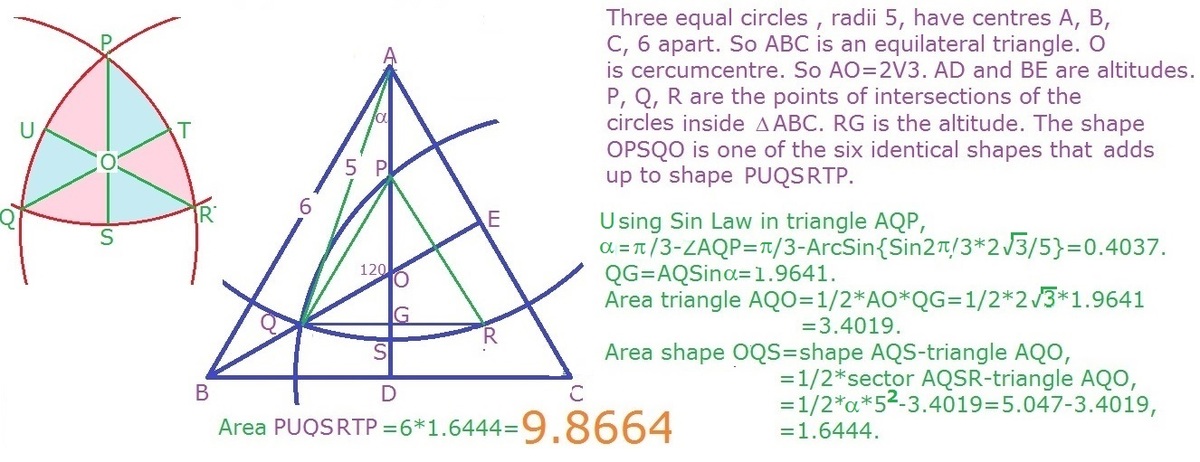
Under laying idea is the same as that of Mr Marta Reece .
 The centers of the circles, labeled
A
,
B
,
C
form an equilateral triangle with side
6
.
The centers of the circles, labeled
A
,
B
,
C
form an equilateral triangle with side
6
.
△ A D C has sides 5 , 5 , and 6 , so ∠ C A D = a r c c o s ( 2 × 5 × 6 5 2 + 6 2 − 5 2 ) = 5 3 . 1 3 ∘
∠ D A B = 6 0 ∘ − ∠ C A D = 6 . 8 7 ∘
∠ E A D = 6 0 ∘ − 2 × ∠ D A B = 4 6 . 2 6 ∘
From △ A E D the distance E D = 5 2 + 5 2 − 2 × 5 × 5 × c o s ( 4 6 . 2 6 ∘ ) = 3 . 9 3
△ D E F is equilateral with area A t = 4 3 × 3 . 9 3 2 = 6 . 6 8
To this we need to add areas of the three identical circular segments. Area of one of them is
A c = 2 R 2 ( 1 8 0 α π − s i n α ) = 2 5 2 ( 1 8 0 4 6 . 2 3 ∘ π − s i n ( 4 6 . 2 3 ∘ ) ) = 1 . 0 6
So the total area is A t + 3 × A c = 6 . 6 8 + 3 × 1 . 0 6 = 9 . 8 7
For radius(r) and distance between circles centers(d), use the following expressions for the common chord (c) and intersection area (A)
c^2=3r^2 - (d^2/2) -d{√(3r^2-(3/4)d^2)}
A=(√3/4)c^2+3[r^2(arcsin (c/2r))-(c/4){√(4r^2-c^2)}]
and using r=5 and d=6, Answer is A=9.865