Intersection of e^x and x!
Find the positive value for which the graph of e x intersects with the graph of Γ(x+1).
(Find the positive value of x which e x = Γ ( x + 1 ) ).
Hint: Γ ( x + 1 ) = x !
The answer is 5.29.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Ah I think I see the confusion. This graph is kind of mislead. x ! should looks like this .
x ! is only defined for whole numbers. For any other numbers, classical gamma function is assumed but not necessary.
Plot [ e y + 5 . 2 9 0 3 1 6 0 9 3 1 1 9 7 7 1 2 4 5 7 6 7 4 2 4 2 6 1 4 3 0 2 7 8 4 2 0 4 4 8 3 0 3 2 2 2 6 5 6 2 − ( y + 5 . 2 9 0 3 1 6 0 9 3 1 1 9 7 7 1 2 4 5 7 6 7 4 2 4 2 6 1 4 3 0 2 7 8 4 2 0 4 4 8 3 0 3 2 2 2 6 5 6 2 ) ! , { y , − 1 0 0 0 0 0 0 1 , 1 0 0 0 0 0 0 1 } ]

Plot [ e x − x ! , { x , 0 , 5 . 3 } ]
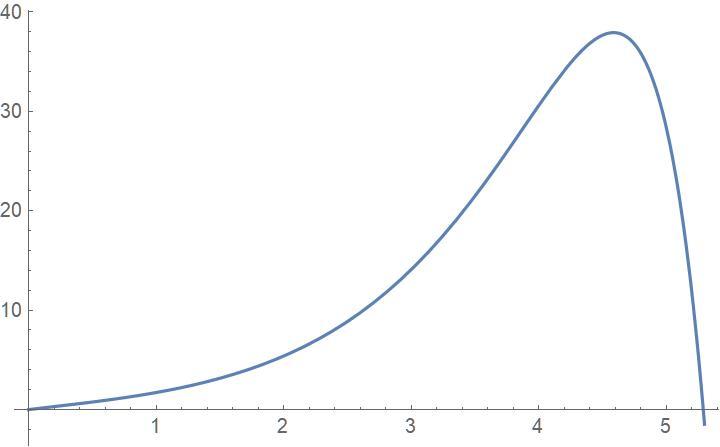
I offer my apologies! This problem fooled me -- I did not look far enough out.
I did not believe that there is a closed form solution. A closed form solution was not requested! I found the answer by first doing some plots and then doing a root search in the vicinity of 5.3 where the plots indicated that there might be a solution in positive x .
x≈5.29