Intersection of two tetrahedrons
Two identical regular tetrahedrons of edge length equal to 10, have the same center and are oriented symmetrically with respect to each other, such that the 4 vertices of one tetrahedron lie on the normals drawn from the centers of the faces of the other tetrahedron, as the figure below illustrates.
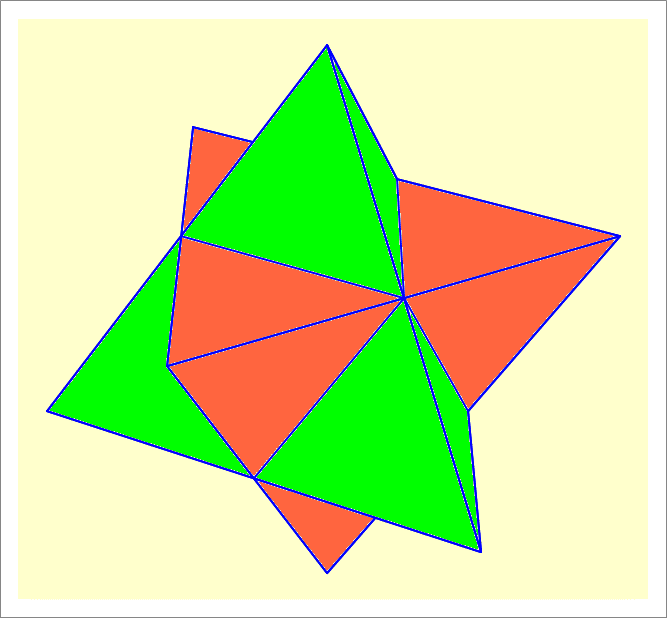
The solid resulting from their intersection is a regular octahedron. Find its volume.
The answer is 58.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Do you think it's level 4?
The volume of each of the given tetrahedra is V = 6 2 1 0 3 . The volume of the intersection is 2 V ≈ 5 8 . 9 3 since we are losing the four ochre tetrahedra each of which has a volume of 2 3 V .
spot on sir!
The side of the regular octahedron is the midsegment of one of the tetrahedron's triangular faces, so it is half the the length of one of the tetrahedron's side, which is s = 2 1 ⋅ 1 0 = 5 .
The volume of a regular octahedron with side s is V = 3 2 s 3 , so its volume is V = 3 2 ⋅ 5 3 ≈ 5 8 . 9 .