Intersection
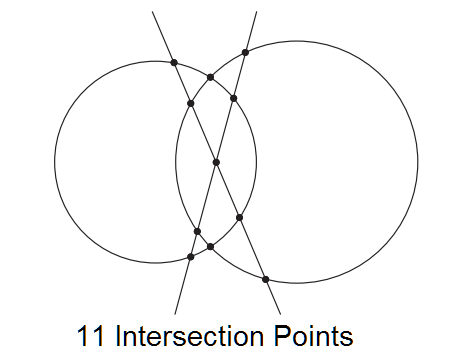 Mary drew two circles and two distinct lines (figure above). She got 11 intersection points. If she draws three more distinct lines, what is the maximum number of intersection points that she can get in total (including the original 11)?
Mary drew two circles and two distinct lines (figure above). She got 11 intersection points. If she draws three more distinct lines, what is the maximum number of intersection points that she can get in total (including the original 11)?
Problem from OBMEP 2015.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
A recursive approach is a good way to solve this problem. I've cleaned up the phrasing slightly, so that it is easier to understand what you mean.
That is exactly what I did but for some reason I did the arithmetics wrongly in my head because I'm too lazy to take a pen and do it properly.
That's what I did ... Whilst sitting on the loo :-)
With m lines and n circles, as a maximum, we can have each pair of lines intersect at a distinct point, each line and circle intersect at two distinct points and each pair of circles intersect at two distinct points. Thus the maximum number of distinct points of intersection is
P ( m , n ) = ( 2 m ) + 2 ∗ ( 1 m ) ( 1 n ) + 2 ∗ ( 2 n )
⟹ P ( m , n ) = 2 m ( m − 1 ) + 2 m n + n ( n − 1 ) .
For Mary's first drawing we have m = 2 , n = 2 and thus
P ( 2 , 2 ) = 2 2 ∗ 1 + 2 ∗ 2 ∗ 2 + 2 ∗ 1 = 1 1 .
Since Mary's initial drawing achieves the maximum possible number of points of intersection for two lines and two circles, it is still possible to achieve the maximum P once three more lines are drawn. We would then have m = 5 , n = 2 and
P ( 5 , 2 ) = 2 5 ∗ 4 + 2 ∗ 5 ∗ 2 + 2 ∗ 1 = 3 2 points of intersection.
With just 2 circles, the number of intersections are 2 when no. of line is 1, the line can intersect the circle at 4 points (2 each) when there are 2 lines, the line can intersect at 4 points, plus cutting the previous line, so 5. for 3 lines, it follow the same pattern, 4 plus cutting the previous 2, so 6 and so on,. so the answer is 2+4+5+6+7+8=32
From marys first drawing we have two circle and 2 lines that intersects the two circle so P(m,n) m as lines and n as number of your circle.. P(m,n)=m(m-1)/2 + 2mn + n(n-1) P(2,2)=2 (2-1)/2+2 (2)(2)+2 (2-1) = 1+8+2 So P(2,2)=11 Now if she will add more three lines we have P(5,2)=5 (5-1)/2 + 2 (5)(2)+2(1) =5 (4)/2 + 20 + 2 P(5,2)=10+20+2 Therefore P(5,2)=32..Ans.
i was not as creative as you guys so i solved with trial and error (with mental drawings because im lazy so i actually got 31 but chose 32). but in hindsight i find that i only chose straight lines. while i imagine curved lines would cause many more intersections. what about that everyone? what does everyone think?
That is true. The question should probably have specified that all the lines apart from the circles are supposed to be straight. With curved lines you can have as many intersections as you like (just scribble).
Log in to reply
She specified in the diagram , you may see that there are three straight lines so assuming straight ...
Brian Charlesworth's solution is amazing, but I have a simpler one. A line can intersect with a circle at 2 points at most, and two lines can intersect at one point. So the first extra line Mary draws can cross 6 points in total (2*2=4 from circles and 2 from lines).
For the second extra line, it similarly can cross 6 points, except we now have the first extra line, so this gives us 6 + 1 = 7 points.
For the third extra line, it similarly can cross 6 points, except we now thave the first and second extra line, so this gives us 6 + 2 = 8 points.
So first, second and third lines can intersect with 6, 7 and 8 distinct points respectively. If we add those to the 11 initial points we had, we obtain 11+6+7+8=32 points in total.