Intersections between chords
On a circle circumference, we choose 50 points and draw all chords joining these points. Find the maximum number of intersections between these chords?
Hint: when the number of points is 5, the maximum number of line intersections is 5.
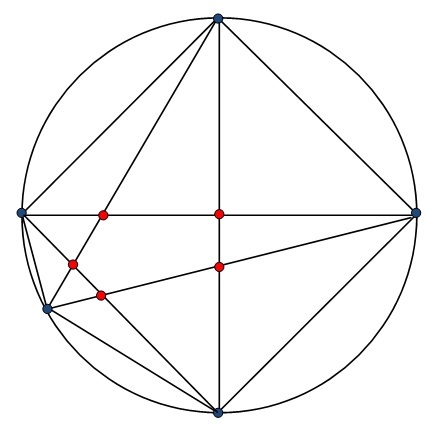
The answer is 230300.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The intersection point of two chords is defined by four points, namely the two end-points of one chord, and the two end-points of the other chord. Conversely, if we take any four points on the circle, then there is exactly one way to draw two chords so that they form an intersection point. This means that the intersection points are in 1-1 correspondence with the number of ways of choosing four points, which is ( 4 5 0 ) = 2 3 0 3 0 0 .
( @starwar clone )