Intervals and stakes ?
1000 balls are set on a straight line. The balls are perfectly spherical. (We do not need in this exercise to consider the interior of each ball.) Each diameter is 1 meter. Each distance between two neighbouring balls is 1 meter.
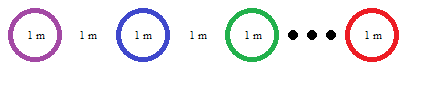
What is the distance between the leftmost point of the leftmost ball and the rightmost point of the rightmost ball ?
The answer is 1999.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Each ball has a diameter of 1 m and the distance between each sphere is 1 m . This means, except the last ball every sphere has a separation of 1 m to its right. So,
Distance between the first and the last points = 2 × ( N u m b e r o f b a l l s − 1 ) + d i a m e t e r o f t h e l a s t b a l l
⟹ 2 × ( 1 0 0 0 − 1 ) + 1
⟹ 2 × 9 9 9 + 1
⟹ 1 9 9 8 + 1 = 1 9 9 9