Into the Pyramid

Geometry Level 3

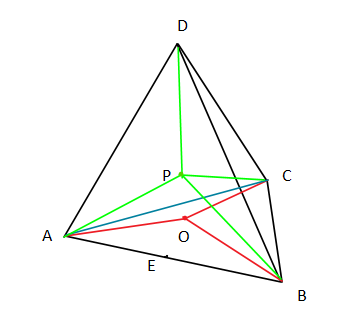The diagram above shows a triangular pyramid with equal edges and faces, and $A, B, C, D$ are its vertices.

Let $E$ be the midpoint of $AB$ , $O$ be the center of the equilateral triangle base, and $P$ be the center of the 3-D pyramid.

What are the ratios of $CO : OE$ and $DP : PO$ respectively?

2:1 \quad,\quad 4:1

2:1 \quad,\quad 2:1

3:1 \quad,\quad 2:1

2:1 \quad,\quad 3:1

3:1 \quad,\quad 4:1

3:1 \quad,\quad 3:1

1 solution

Eggz D
Jun 25, 2020

$\overline{CO} : \overline{OE} = x : x\times sin30$ as shown by the 30 degree triangle created below: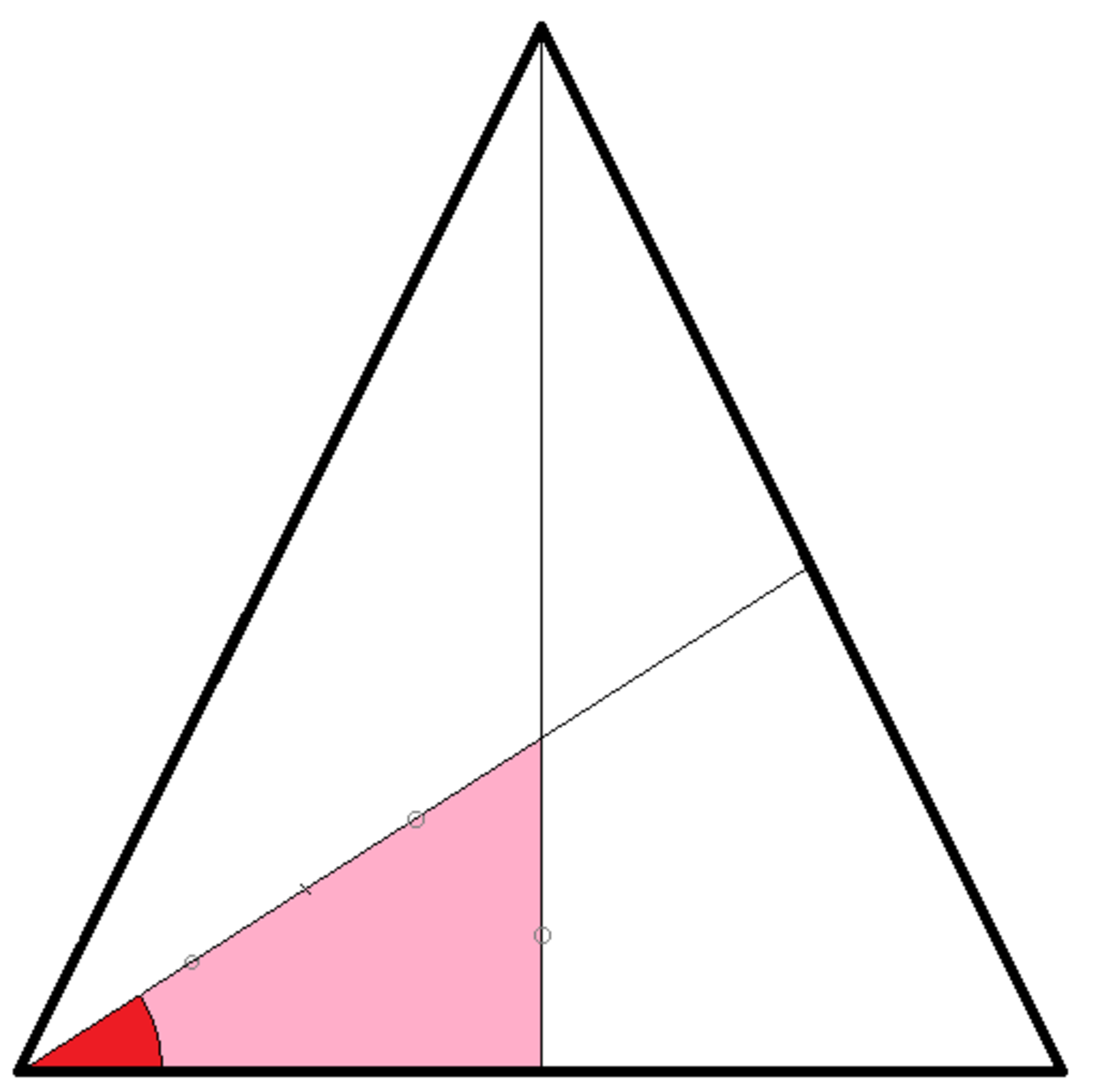

$\overline{DP} : \overline{PO}$ can be solved in the same way but i prefer this method:

P is the Center of Mass

The Volume of a Prism is $Area \times height$ ; the Pyramid's Volume is $\frac{Area \times height}{3}$

The Mass is directly related to the height of the Pyramid, we can derive that the Center of Mass is $1 : 3$ up it's height.