Intro to three phase systems - 3 -
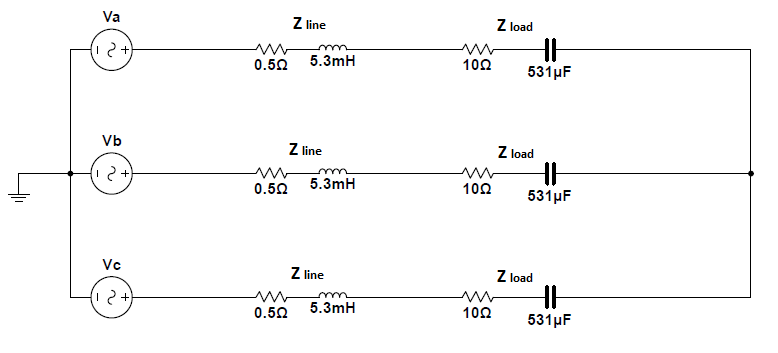
A symmetrical three-phase system is shown in the image. Considering positive sequence, V a n = 1 2 0 ∠ 0 ∘ and ignoring mutual impedance, what are the phasors for the phase voltage across the load?
Details and Assumptions:
- f = 6 0 H z
- α = 1 ∠ 1 2 0 ∘
- Positive sequence is the sequence ABC
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the three-phase system is symmetrical, we need only consider one phase. The phase voltage across the load is given by:
V load = Z line + Z load Z load × V a n = 0 . 5 + 2 π × 6 0 × 5 . 3 × 1 0 − 3 j + 1 0 − 2 π × 6 0 × 5 3 1 × 1 0 − 6 1 j 1 0 − 2 π × 6 0 × 5 3 1 × 1 0 − 6 1 j × 1 2 0 = 0 . 5 + 2 j + 1 0 − 5 j 1 0 − 5 j × 1 2 0 = 1 0 . 5 − 3 j 6 0 0 ( 2 − j ) = 1 0 . 9 2 ∠ − 1 5 . 9 4 ∘ 1 3 4 1 . 6 4 ∠ − 2 6 . 5 6 ∘ ≈ 1 2 2 . 8 6 ∠ − 1 0 . 6 ∘
Since the clockwise sequence is ⎣ ⎡ 1 α 2 α ⎦ ⎤ , the phasor is 1 2 2 . 8 6 ∠ − 1 0 . 6 ∘ ⎣ ⎡ 1 α 2 α ⎦ ⎤ .