Introducing Disphenoid
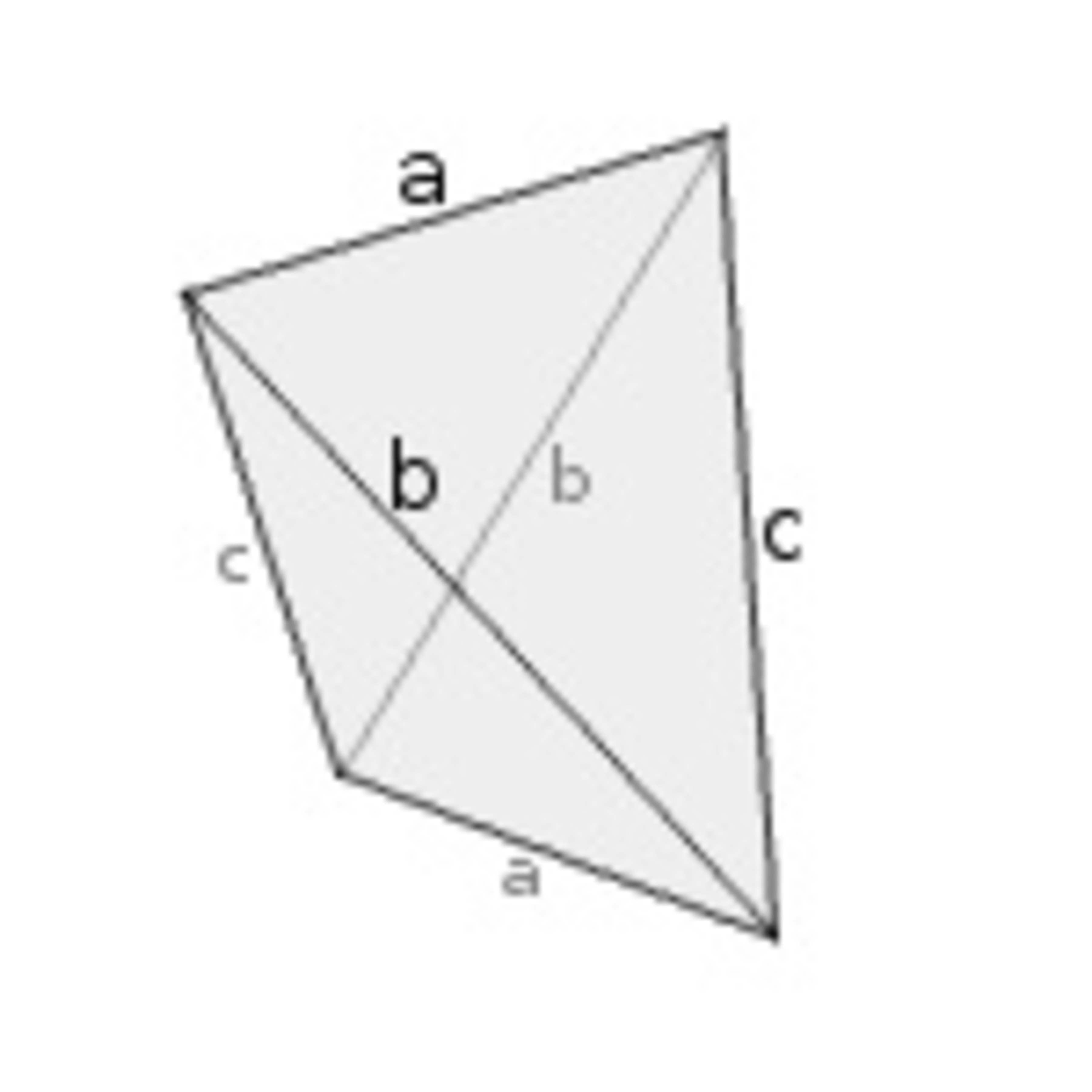
A disphenoid is a non-regular tetrahedron whose faces have the same perimeter/area, and thus consist of congruent triangles.
For a disphenoid with edge lengths to exist, the value of must strictly be greater than...
Do you want more? Try this
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The formula for the volume V of disphenoid given its edge lengths a , b , and c is:
V = 7 2 ( a 2 + b 2 − c 2 ) ( a 2 − b 2 + c 2 ) ( − a 2 + b 2 + c 2 )
Substituting for values in terms of x, we get
V = 7 2 ( x 2 + 2 x + 3 ) ( x + 5 ) ( x − 3 ) ( x + 1 ) 2
It will be clear from here when V becomes imaginary, when it becomes zero, and when it becomes a positive real number. :)