Introduction to The Modulus Function
Let f ( x ) = x 2 − 2 x and g ( x ) = x 2 − 4 x + 4 .
How many real solutions does the equation ∣ f ( x ) ∣ = g ( ∣ x ∣ ) have?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
You really should restate the problem to only admit real solutions. There is also one complex-conjugate pair x = +/- 0.59829i (which makes 5 solutions in total).
Read about absolute values here .
Here's a more visual approach to the problem.
First, let's sketch the graphs of f ( x ) , ∣ f ( x ) ∣ , g ( x ) and g ( ∣ x ∣ ) .
You can sketch f ( x ) and g ( x ) by solving f ( x ) = 0 and g ( x ) = 0 to find the x intercepts , and letting x = 0 to find the vertical intercept .
Then, to sketch ∣ f ( x ) ∣ , reflect any parts of the graph of f ( x ) that are below the x axis in the x axis .
Finally, to sketch g ( ∣ x ∣ ) , sketch g ( x ) for x = 0 and x > 0 , and then reflect this in the y axis .
This process is shown below:
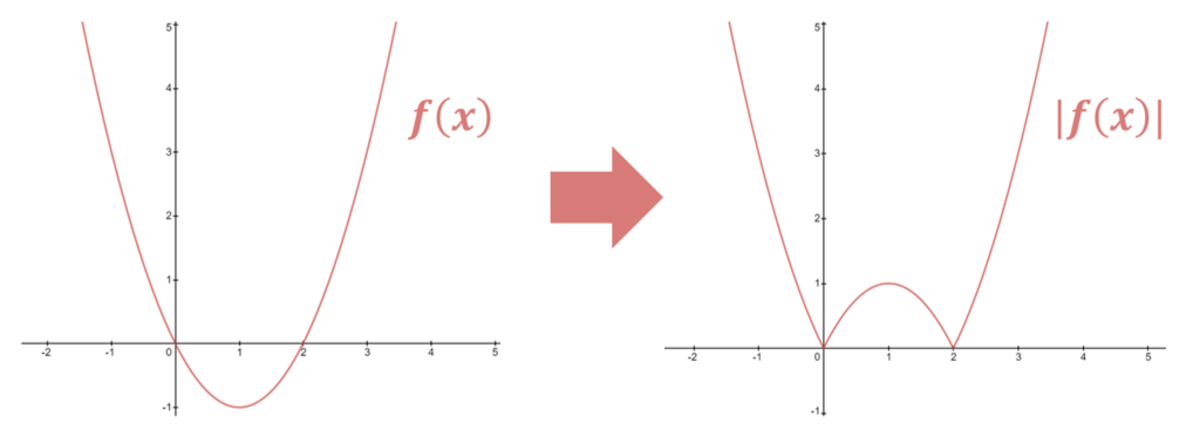
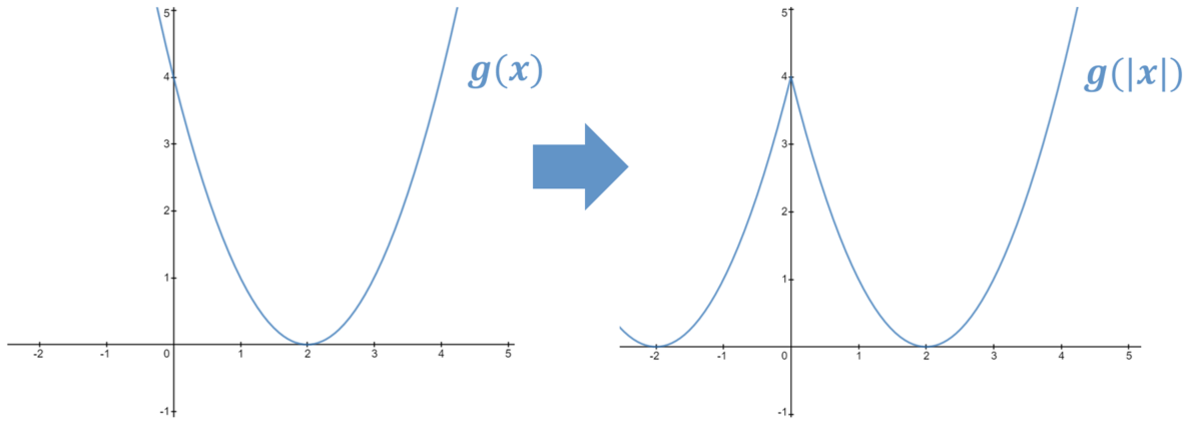
If we superimpose the graphs of ∣ f ( x ) ∣ and g ( ∣ x ∣ ) , we can see where they intersect :
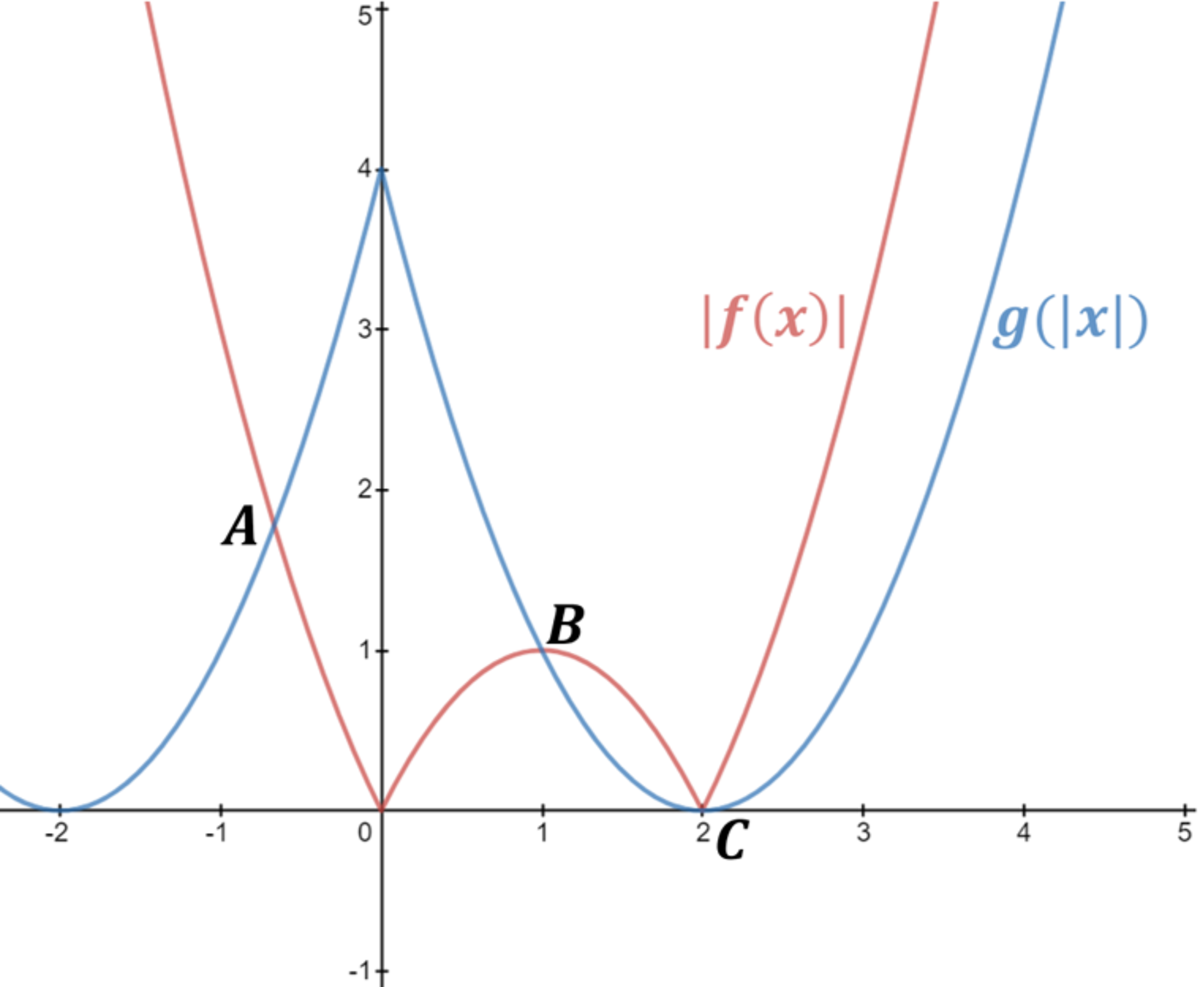
| There are 3 points of intersection, so the equation ∣ f ( x ) ∣ = g ( ∣ x ∣ ) has 3 solutions . |
Bonus : find the coordinates of A , B and C .
Since f ( x ) = x 2 − 2 x = x ( x − 2 ) , theb f ( x ) < 0 when 0 < x < 2 and we have:
∣ f ( x ) ∣ = { x ( 2 − x ) = 2 x − x 2 x ( x − 2 ) = x 2 − 2 x if 0 ≤ x < 2 elsewhere
Note that
g ( ∣ x ∣ ) = ∣ x ∣ 2 − 4 ∣ x ∣ + 4 = { x 2 − 4 x + 4 x 2 + 4 x + 4 if x ≥ 0 if x < 0
Therefore
∣ f ( x ) = g ( ∣ x ∣ ) = ⎩ ⎪ ⎨ ⎪ ⎧ x 2 − 2 x = x 2 + 4 x + 4 ⟹ x = − 3 2 2 x − x 2 = x 2 − 4 x + 4 ⟹ x = 1 x 2 − 2 x = x 2 − 4 x + 4 ⟹ x = 2 if x < 0 if 0 ≤ x < 2 if x ≥ 2
There are 3 solutions.